Оптимизация технологических задач

Инженеру – проектировщику приходится решать оптимизационные задачи, так как его работа прежде всего направлена на разработку новых более эффективных производственных систем: технологических процессов и средств их оснащения, прогрессивного оборудования и машин.

Под математической оптимизацией обычно понимают совокупность различных математических методов, алгоритмов и программ, направленных на нахождение оптимума функции, наиболее полно характеризующей потребительские свойства рассматриваемого объекта. Такую функцию в теории оптимизации называют целевой функцией, а ее аргументы, за счет рационального выбора которых достигают или приближаются к оптимуму называют проектными параметрами.

Число проектных параметров может быть различно. Если такой параметр один, тогда оптимизируют функцию одной переменной, – решают задачу одномерной оптимизации. Если проектных параметров несколько, – решается задача многомерной оптимизации. Так как проектные параметры в технологических задачах принимают главным образом вещественные значения, то каждому набору этих значений, можно поставить в соответствие вектор n-мерного эвклидового пространства Rⁿ.

Исходя из физического смысла, технико-экономических возможностей в технологических процессах, исследуемые параметры не могут принимать любые численные значения и на них должны быть наложены ограничения.

В результате этого, можно предложить обобщенную математическую формулировку задач оптимизации – найти оптимум функции:

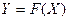, (28.1)

в которой Х=(х₁,х₂,…,х_n) – n-мерный вектор проектных параметров х_i. При условии существования следующих ограничений:

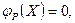
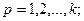(28.2)

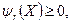
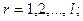(28.3)

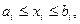
(28.4)

где k – число ограничений – равенств, l – число ограничений – неравенств, a_i и b_i – границы варьирования проектных параметров x_i, зависящие от конкретных условий задачи.

Если ограничения (28.2) – (28.4) не наложены (k=0, l=0, a_i=- 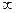, b_i=+ 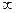), то имеют дело с задачей безусловной оптимизации функции (28.1). В противном случае рассматривают задачу условной оптимизации.

Лекция №29