Индивидуальное моделирование

В отличие от ранее рассмотренных методик построения имитационных моделей будем понимать под индивидуальным моделированием такие разработки имитационных моделей, которые носят сугубо индивидуальный, уникальный характер. Это имитационные модели, разработанные для исследования конкретных систем.

Рассмотрим пример такой имитационной модели, позволяющий исследовать функционирование простейшего склада. Пусть на нем обеспечивается поступление, хранение и выдача потребителю некоторой детали. Для полноты картины будем считать, что все процессы, описывающие поведение склада, носят вероятностный характер. Ясно, что детерминизация какого-либо процесса приведет лишь к упрощению модели.

Введем следующие обозначения (рис.27.1):

Рис.27.1. Простейший склад.

t - текущее время, t=1,2,…,

S_t - состояние склада в момент времени t,

S_min - минимально допустимое состояние склада,

S_max - максимально допустимое состояние склада,

R_p - сигнальный уровень (R_p≥0),

ε_t - спрос на деталь в момент времени t (ε_t ≥ 0),

Q_i - размер поставки деталей от поставщика (Q_i≥0),

τ_j - время выполнения заказа на поставку (τ>0),

p - вероятность дефицита детали.

При поступлении спроса ε_t в момент времени t состояние склада S_t уменьшается на величину этого спроса. При достижении состоянием склада некоторого сигнального уровня R_p вырабатывается запрос потребителю на поставку партии деталей. Через случайное время τ эта партия размером Q_i поступит на склад и увеличит его состояние. Сигнальный уровень предназначен для управления процессом пополнения содержимого склада. В процессе функционирования склада возможна ситуация дефицита, когда состояние склада S_t может стать отрицательным (в математическом смысле). Это возможно в том случае, если в процессе потребления содержимое склада будет исчерпано, а поставка партии деталей не произошла. Для управления состоянием склада будем использовать параметр р – вероятность дефицита.

Ясно, что система должна быть построена и должна работать так, чтобы, по возможности, избежать дефицита. Очевидно, что при нулевой вероятности дефицита р сигнальный уровень R_p должна равняться бесконечности. Таким образом, ясно, что сигнальный уровень обратно пропорционален вероятности дефицита. С практической точки зрения ограничим сигнальный уровень интервалом

S_min ≤ R_p ≤ S_max.

Обратимся к экономической сущности задачи. С этой точки зрения интервал [S_min, S_max] должен быть как можно меньше. Это объясняется тем, что уровни S_min и S_max должны быть как можно меньше, так как они определяют объемы материальных ценностей, не задействованные в процессе производства, то есть характеризуют уровень пролеживающих оборотных средств. Исходя из этого уровни S_min и S_max должны быть устремлены к нулю.

Одновременно, для того, чтобы обеспечить бездефицитное функционирование склада необходимо устремить S_min и S_max к бесконечности.

Таким образом, сигнальный уровень R_p как средняя величина интервала [S_min, S_max] с одной стороны должен быть как можно больше, с другой, - равен нулю.

Сигнальный уровень R_p как параметр, зависящий от случайных явлений (τ_j, Q_i, ε_t), носит также случайный характер. Поэтому для него справедливо понятие доверительного интервала с границами

R_p ± k·σ(S_t),

где коэффициент k определяет размер доверительного интервала.

Исходя из того, что для интервала [S_min, S_max] известно одно значение - S_min=0, можно заключить, что

R_p = k·σ(S_t). (27.1)

Для определения среднеквадратического отклонения состояния склада S_t воспользуемся очевидной формулой

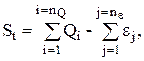
где n_Q – количество поставок за время от 0 до t,

n_ε – количество спросов за время от 0 до t.

В этом выражении все, входящие в него величины, являются случайными и каждое слагаемое есть сумма случайного числа случайных величин.

Видно, что для суммы (Y) случайного числа (n_x) случайных величин (X_j)

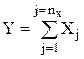
математическое ожидание определяется выражением

M[Y] = M[n_x] · M[X],

а среднеквадратическое отклонение

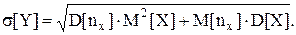
Подставив последнее выражение в (4.27)

.

А так как мы выяснили, что сигнальный уровень R_p и вероятность дефицита р обратно пропорциональны, то можно полагать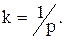

Таким образом,

(4.28)

Отметим, что приведенные выше рассуждения являются единичным и совершенно не характерным способом определения сигнального уровня и параметров работы склада. Более подробные сведения по этому вопросу можно найти в специальной литературе, посвященной системам управления запасами (ресурсами, материально-техническим снабжением, оперативного планирования и управления производства).

Для полноты описания исследуемой системы следует провести сбор и обработку статистической информации, описывающей поведение случайных процессов спроса (ε_t) и поставок (Q_i и τ_j) в реальной системе. Выявленные вероятностные свойства необходимы для воспроизведения случайных чисел ε_t, Q_i и τ_j в процессе имитационного эксперимента. С точки зрения системных исследований рассматриваемого объекта сбор реальных данных может и не производиться. Мы можем воспользоваться описанными выше методами воспроизведения случайных чисел с задаваемыми нами, необходимыми для исследования вероятностными свойствами.

Оценка адекватности имитационной модели реальной системе является чрезвычайно важным этапом. Обусловлено это тем впечатлением реальности, которым обладают описываемые модели, и проверка, выполненная без должной тщательности, может привести к тяжелым последствиям.

Проверка соответствия модели и объекта заключается в сравнении интересных для исследователя свойств оригинала и модели.

Для этого необходимо исследовать функциональную или проектируемую систему, что естественно, не всегда возможно. Таким образом, не всегда возможна прямая экспериментальная проверка адекватности свойств модели и объекта.

Вместе с тем, адекватность не следует непосредственно из процесса построения модели. Упрощенная модель не может быть подобна объекту в смысле, обычном для теории подобия: требование пропорциональности сходных параметров и процессов в модели и объекте заведомо не соблюдается из-за различия в числе параметров.

Тем не менее, в литературе рассматриваются различные способы оценки адекватности имитационной модели реальной системы. В частности, предлагается использовать проверки на качество результатов при задании предельных значений исходных данных, на верность исходных предположений и на правильность преобразования информации в модели.

Лекция №28