Многомерная безусловная оптимизация

Задачи многомерной безусловной оптимизации формули­руются аналогично общей задаче оптимизации при отсутствии ограничений (28.2)-(28.4). Необходимым условием существования экстремума целевой функции 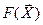в точке 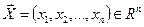n - мерного пространства проектных параметров является обращение в нуль компонент вектора-градиента функции в этой точке:

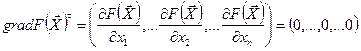(30.1)

В общем случае условие стационарности (30.1) точки, про­странства Rⁿ обозначаемой 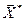определяется путем решения не­линейной системы уравнений:

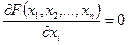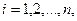; (30.2)

что представляется весьма трудоемкой задачей.

Достаточное условие существования экстремума целевой функции в точке 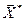задается результатами исследования матрицы Гессе:

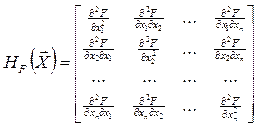(30.3)

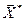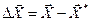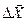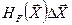Для максимума целевой функции достаточным условием является то, что матрица Гессе (30.3) в стационарной точке , при любом векторе будет отрицательно определенной, т.е. скалярное произведение и – отрицательно, а для минимума – положительно определенной т.е. произведение 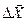и 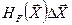– положительно. В противном случае экстремум в 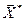не достигается, а сама стационарная точка – седловая.

Нахождение точек оптимума F(X) путем анализа выше условия (30.2) и исследование матрицы (30.3) даже в двумерном слу­чае 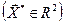вы­зывает существенные затруднения. Поэтому разработаны математические методы и алго­ритмы, позволяющие достаточно простыми способами при­ближаться к оптимуму.

Один из наиболее наглядных, широко применяемый на практике метод безусловной оптимизации – симплексный поиск.

Регулярным симплексом в пространстве Rⁿ называют пра­вильный многогранник, образованный п+1 равноотстоящими друг от друга вершинами. Так, например, на координатной плоскости, в пространстве (R²) симплекс – правильный тре­угольник, в трехмерном пространстве (R³) – тетраэдр.

Координаты (п штук) вершин (п+1 штука) регулярного симплекса задаются матрицей размером (п+1)´п

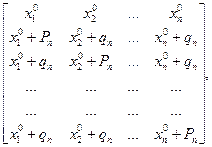
где X⁰ – так называемая базовая вершина симплекса, выбор которой осуществляют на основании априорной информации о поведении целевой функции. Постоянные Р_n и q_n находят по следующим формулам:

.

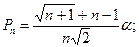
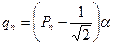Масштабный множитель α равный длине стороны симплекса также вы­бирается исходя из предварительной информации о поведении целевой функции.

После построения начального симплекса – определения координат его вершин (рис.30.1,а), находят такую вершину (x₁,x₂,…,x_n), в которой целевая функция имеет наибольшее значение (при отыскании минимума), и отображают ее симметрично центру тяжести остальных вершин симплекса.

Коорди­наты центра тяжести Х^{ц т}вершин симплекса вычисляют по формуле

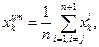
где j – номер отображаемой вершины; k=1,2,…,n.

Координаты новой вершины симплекса 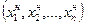определяют по формуле

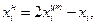
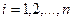
Затем вычисляют значение целевой функции во вновь полу­ченной вершине 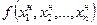и сопоставляют со значе­ниями в остальных вершинах симплекса за исключением от­раженной вершины. Вновь разыскивается худшая вершина, отображается относительно центра тяжести остальных и т. д. (рис.30.1, б).

Если после очередного отражения вершины не достига­ется приближение к экстремуму целевой функции при до­статочно малой длине ребра симплекса, то поиск можно пре­кратить. За искомое экстремальное значение в этом случае принимают наименьшее (в случае поиска максимума-наи­большее) значение целевой функции в вершинах последнего из построенных симплексов. Если заданная точность шага длина ребра не удовлетворяет, то выбрав нужную вершину в качестве базовой, уменьшают в требуемой степени масштабный коэффициент α и про­должают симплексный поиск.

Известна модификация симплексного поиска, позволяю­щая последовательно растягивать и сжимать длину ребра симплекса именуемая процедурой Нелдера-Мида.

Симплексный поиск может быть использован и как метод планирования эксперимента. В этом случае информацию о значениях целевой функции находят экспериментально при величинах проектных параметров, со­ответствующих координатам вершин симплекса.

К числу достоинств симплексного поиска следует отнести простоту алгоритма и расчетных формул, отсутст­вие сильной чувствительности к характеру изменения целе­вой функции.

В то же время метод оптимизации на симплексе имеет ряд недостатков. Алгоритм работает относительно медленно, так как количественная информация о значениях целевой функции в вершинах симплекса не используется. При необ­ходимости изменить длину ребра симплекса требуется за­ново рассчитать значения целевой функции во всех верши­нах вновь построенного симплекса с новой длиной ребра.

От первого из указанных недостатков свободны градиент­ные методы поиска. В отличие от симплексного поиска при использовании этой группы методов требуется предваритель­ная информация о дифференцируемости целевой функции. Для нахождения точки оптимума в пространстве проектных параметров Rⁿ используют итеративную процедуру:

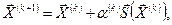
где 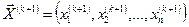–вычисленное на данном шаге приближение к оптимуму вектора проектных параметров; 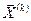–текущее значение вектора проектных па­раметров; α^(k) – текущее значение параметра, характеризую­щего длину шага; 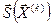–направление поиска на текущем шаге.

Выбор векторов 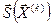осуществля­ют на основании информации о частных производных целевой функции по проектным параметрам. Выбор числового параметра α^(k) на каждом шаге ведут обычно, решая задачу оптимизации целевой функции в направлении .

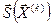Из всего многообразия методов многомерной оптимизации рассмотрим относительно простые методы поиска минимума целевой функции .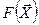

Метод координатного спуска заключается в поочередном поиске минимума по координате x₁, затем x₂ и т.д. поиск ведется с одинаковым шагом, который уменьшается после нахождения всех значений x_1m, x_2m, …, x_nm.

Метод координатного спуска с квадратичной интерполяцией – экстраполяцией основан на последовательном поиске минимума каждой переменной с применением для этого метода квадратичной интерполяции – экстраполяции.

Метод спирального координатного спуска отличается тем, что шаг меняется каждый раз при переходе от поиска минимума по одной переменной к поиску по другой. Обычно это дает некоторое сокращение времени поиска и в трехмерном пространстве напоминает спуск во впадину по спирали.

Лекция №31