Условная оптимизация линейных моделей

Значительное число задач условной оптимизации требует нахождения оптимума целевых функций, линейно зависящих от проектных параметров. Если при этом и функции, входящие в ограни­чения, также линейны, то для нахождения оптимального ре­шения используют методы линейного программиро­вания (ЛП).

Пусть целевая функция линейно зависит от проектных парамет­ров:

(31.1)

Данную функцию необходимо оптимизировать при наложении m линейных ограничений-равенств:

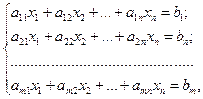(31.2)

Матрица системы (31.2) А={а_ij}, имеющая размерность т×п,называется матрицей коэффициентов; 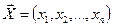— вектор переменных; 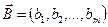— вектор ресурсов; 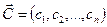— вектор оценок. Дополнительно полагают, что

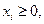
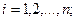
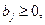
(31.3)

Обычно т<п и система (31.2) имеет мно­жество решений. В результате требуется выбрать такое решение, которое обеспечит оптимум целевой функции (31.1).

Формулировку задачи ЛП в виде (31.1)-(31.3) принято называть стандартной. Как правило имеющие физический смысл, ограничения типа (31.2), накла­дываемые на проектные параметры, представлены нестрогими неравенствами. Кроме того, для некоторых i и j могут не выполняться и условия (31.3). В этом случае с помощью математических пре­образований исходная задача приводится к стандартному виду. Нестрогие неравенства-ограничения превращают в ра­венства (31.2) путем введения дополнительных, называемых остаточными, переменных. Эти переменные в (31.1) имеют нулевые компоненты вектора оценок. Неопределенные по знаку компоненты вектора 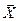представляют в виде разности двух дополнительных переменных, которые предполагают положительными.

Свойство целевой функции задачи ЛП достигать опти­мума в вершинах многогранника области допустимых решений является фундаментальным свойством таких задач. Поэтому для нахождения решения задачи ЛП до­статочно рассчитать значения целевой функции в вершинах гипермногогранника области допустимых решений и выбрать среди них экстремальное. Расчет значений целевой функции жела­тельно вести последова­тельно приближаясь к оптимуму, отбросив, по возможности, как можно больше вершин. Поэтому поиск оптимума задач ЛП ведут по специальным экономичным алгорит­мам.

Наибольшее распространение для решения задач ЛП получил симплекс-метод. Он представляет собой про­цедуру перебора вершин гипермногогранника области допу­стимых решений, осуществляемого так, чтобы на каждом шаге происходило последовательное приближение целевой функции к оптимуму с автоматическим отбрасыванием век­торов проектных параметров, в которых целевая функция удаляется от оптимума.

Сущность симплекс-метода состоит в следующем. С по­мощью процедуры Гаусса-Жордана система ограничений-равенств (31.2) приводится к каноническому виду

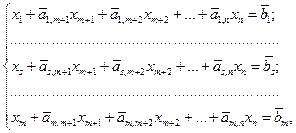(31.4)

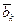где коэффициенты при переменных и свободные члены получены арифметическими операциями над таковыми в (31.2). При этом преобразование (31.2) в (31.4) ведут так, чтобы 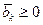, k=1,2,...,т. При обычно имеющем место соотношении т<п система (31.4) имеет множество решений. Принято называть переменные 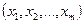базисными, a — небазисными. Базисное решение (31.4) получают при нулевых не­базисных переменных:

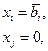
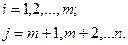(31.5)

Любое базисное решение задает коор­динаты вершины гипермногогранника допустимой области решений, определяемой (31.2) и (31.3).

Для опре­деленности будем предполагать поиск максимума целевой функции. Условие оптимальности базисного решения легко полу­чить, рассчитав приращение целевой функции ΔZ_s, дополни­тельно введя в базис переменную x_s=1, где 1≤s≤п. Преобразовав (31.1), (31.4) и (31.5), можно получить

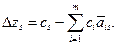(31.6)

Выражение (31.6) называют правилом скалярного про­изведения. Если Δz_s≤0 при s=т+1,…,п, то увеличить целевую функцию не удается. Поэтому пра­вило скалярного произведения (31.6) является критерием опти­мальности базисного решения.

Если существуют такие но­мера s, при которых Δz_s>0, то базисное решение не опти­мально. Тогда производят последовательную замену пере­менных в базисе, добиваясь уменьшения целевой функции. Для этого предполагают, что при s=р приращение Δz_p

Δz_s>0, где т+1≤s≤п.

и вводят x_р в базис. Тогда система (31.2) при­нимает вид

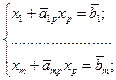(31.7)

Согласно (31.7) с увеличением x_р будут меняться и х_i; i=1,...,m. Возрастание x_р, с одной стороны, приведет к уве­личению целевой функции, с другой, может сделать одну из компонент вектора проектных параметров отрицательной, если 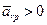. Это недопустимо в силу (31.3). Поэтому

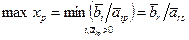
Запись в правой части означает, что перебор для нахожде­ния минимума ведется по таким индексам i, для которых 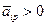. Найдя i=r, обеспечивающее указанный минимум, заме­няют переменную x_r с номером r на переменную x_p. Новое базисное решение, ведущее к увеличению целевой функции, имеет вид

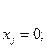
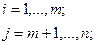
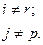
Таким образом, применение симплекс-метода для оптимизации линейной целевой функции задачи ЛП в стандартной форме при наличии базисного решения сводится к следую­щему алгоритму:

1. Вычисляются приращения целевой функции по правилу скалярного произведения.

2. Выбирается среди них максимальное положительное. Если все оценки не положительны, то начальное базисное решение оптимально. Вводится в базис переменная с соответствующим индексом.

3. Опреде­ляется с помощью правила минимального отношения переменная, выводимая из базиса.

4. Строится с помощью элементарных преобразований система канонического вида для нового базиса.

5. Осуществляется переход к началу данного алгоритма и повторяются итера­ции 1-4 до получения оптимального решения.

Лекция №32