Алгоритм метода Гомори решения целочисленных оптимизационных моделей

Рассмотрим полностью целочисленную оптимизационную модель:

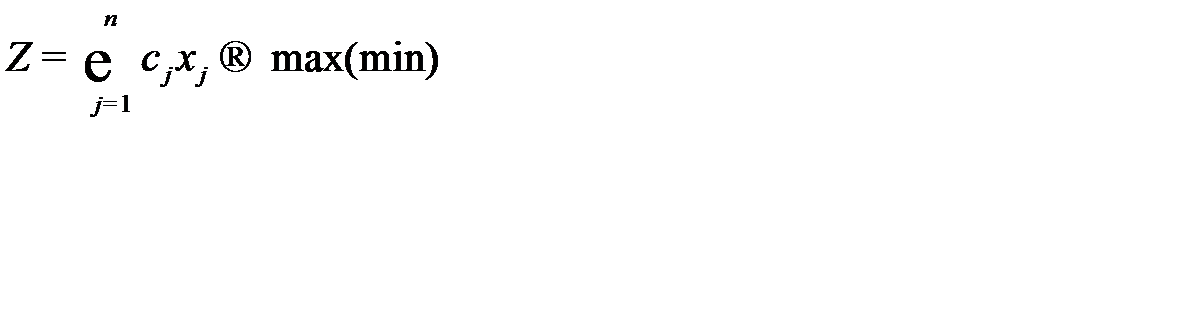
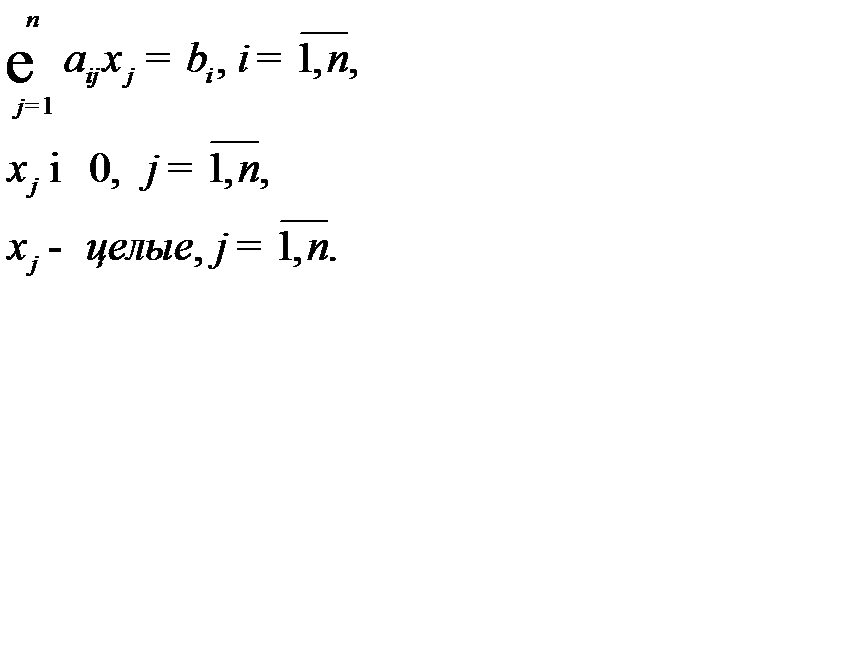
Р.Гомори разработал алгоритм решения целочисленных оптимизационных моделей, в котором вначале используется симплексный метод. А затем, если среди координат найденного оптимального плана имеются нецелые числа, то к ограничениям модели присоединяется дополнительное линейное ограничение, формируемое по специальному правилу, которому не удовлетворяет найденный нецелочисленный оптимальный план, но удовлетворяет любой целочисленный план. Это дополнительное ограничение называется правильным отсечением.

Геометрически каждому дополнительному ограничению соответствует гиперплоскость, отсекающая от многогранника планов некоторую его часть вместе с нецелочисленной оптимальной вершиной. Через конечное число отсечений искомая целочисленная точка окажется сначала на грани, а затем станет вершиной неоднократно усеченного многогранника планов.

Пусть в результате решения симплексным методом канонической целочисленной оптимизационной модели получен оптимальный план ( ), в котором b не целая компонента (см. таблицу 4.1).

Таблица 4.1

Б.П.	А	СП
- … -
	b	b … b
…	…	. . .
	b	b … b
…	…	. . .
	b	b 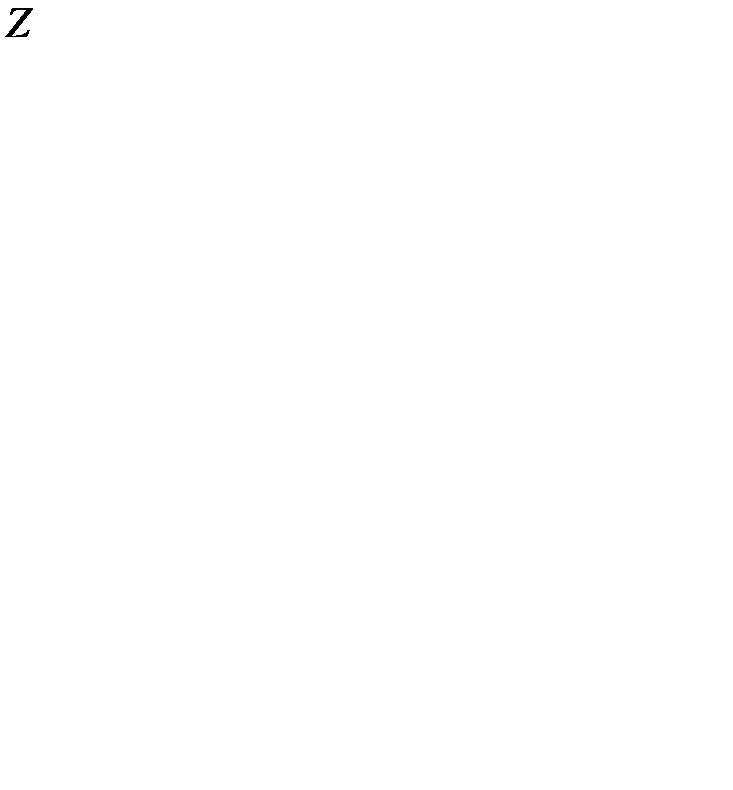… b
=	b	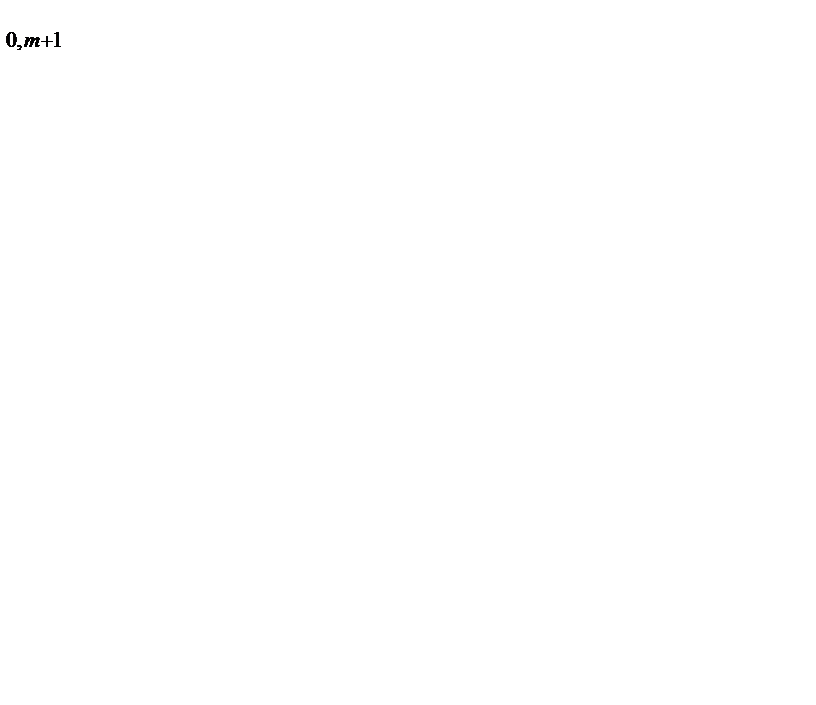b … b

Тогда неравенство:

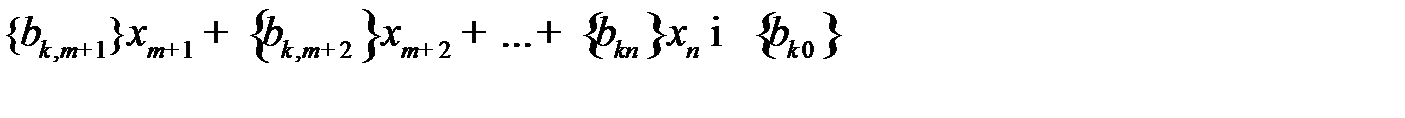(4.1)

сформированное по -ой строке, обладает всеми свойствами правильного отсечения. Символ 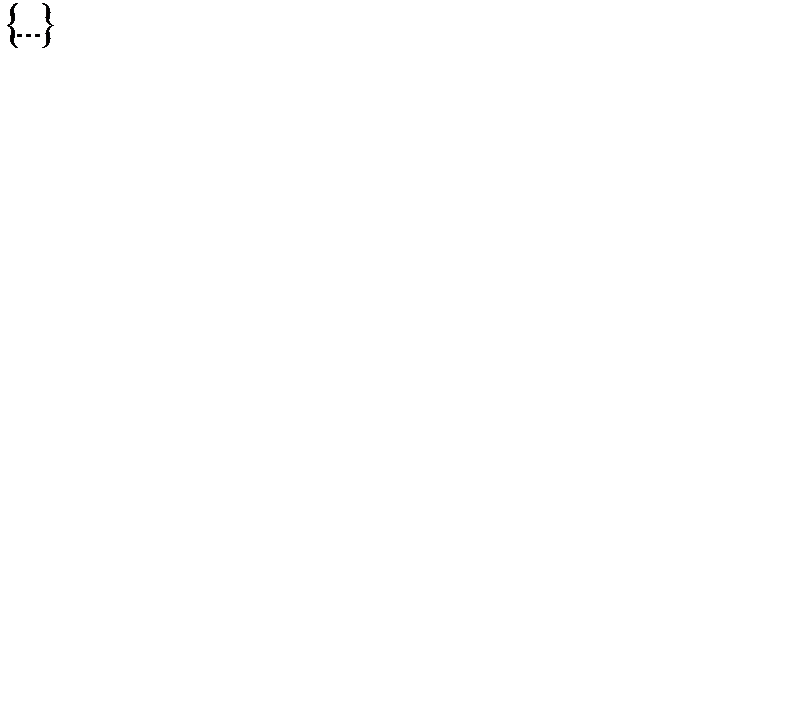означает дробную часть числа: .

Для решения целочисленной оптимизационной модели используется следующий алгоритм:

1. Симплекс-методом решается исходная модель. Если все компоненты оптимального плана целые, то план является оптимальным и для целочисленной оптимизационной модели. Если модель не разрешима, то и целочисленная оптимизационная модель не разрешима. Если среди компонентов оптимального плана есть нецелые, то переходим к пункту 2.

2. Среди нецелых компонент выбирается компонента с наибольшей дробной частью и по соответствующей строке симплексной таблицы, содержащей нецелочисленный оптимальный план, формируется правильное отсечение (4.1).

3. Неравенство (7.1) введением дополнительной неотрицательной целочисленной переменной преобразуется в эквивалентное уравнение

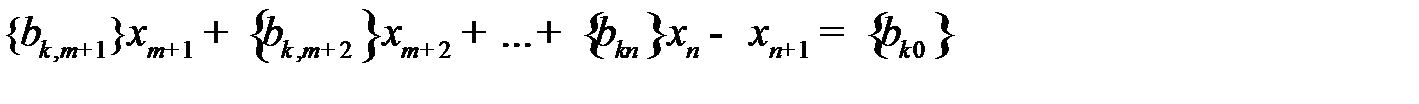, (4.2)

которое включается в систему ограничений.

4. К расширенной системе ограничений вновь применяется симплексная процедура. Если полученный оптимальный план будет целочисленным, то план является оптимальным и для целочисленной оптимизационной модели. Если найденное таким образом решение опять будет не целым, то формируется новое дополнительное ограничение и процесс вычислений повторяется.

Если задача разрешима в целых числах, то после конечного числа итераций целочисленный план будет найден.

Если в процессе решения появится строка с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В таком случае и исходная модель не разрешима в целых числах.

Отметим, что при помощи методов отсечения не целесообразно решать задачи большой размерности, так как число необходимых итераций может быть очень большим.

Пример 4.1. Некоторая фирма покупает оборудование стоимостью 25 ден. ед. Оборудование должно быть размещено на площади не превышающей 10м .Фирма может заказать оборудование двух типов: машины А стоимостью 6 ден. ед., требующие производственную площадь 2м (с учетом проходов) и обеспечивающие производительность за смену 5 ед. изделий и машины типа В стоимостью 7 ден. ед., занимающие площадь 3м и обеспечивающие производительность за смену 6 ед. изделий. Требуется рассчитать оптимальный вариант приобретения оборудования, обеспечивающий при данных ограничениях максимальную производительность.

Решение. Пусть – количество машин типа А; – количество машин типа В.

По условию задачи составим математическую модель:

Найти план приобретения оборудования , при котором целевая функция

и который удовлетворяет ограничениям:

6 + 7 ≤ 25,

2 + 3 ≤ 10,

и - целые числа.

Решим задачу симплексным методом без условия целочисленности переменных в следующих симплексных таблицах.

Б.П.	А	СП
- -
=
=
=		-1 2

Таблица 4.2 Таблица 4.3

Б.П.	А	С.П.
- -
=		6 7
=		2
=		-5 -6

Таблица 4.4

БП		СП

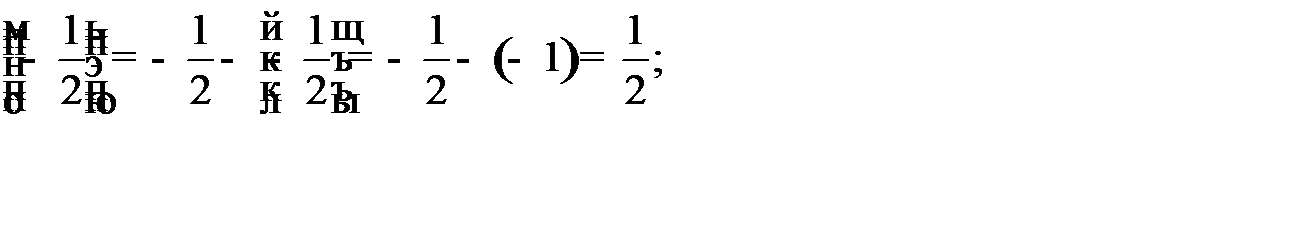
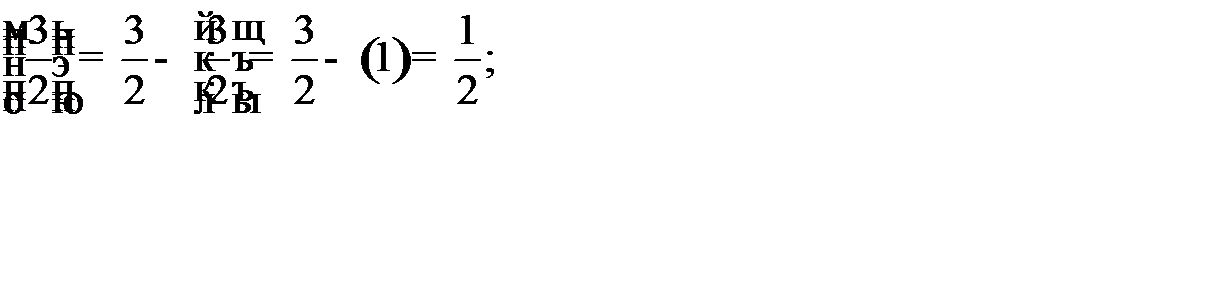
В таблице 4.4 содержится оптимальный, но нецелочисленный план . Среди нецелых свободных членов выбираем , так как это число имеет наибольшую дробную часть равную . По второй строке формируем правильное отсечение: . Находим дробные части: 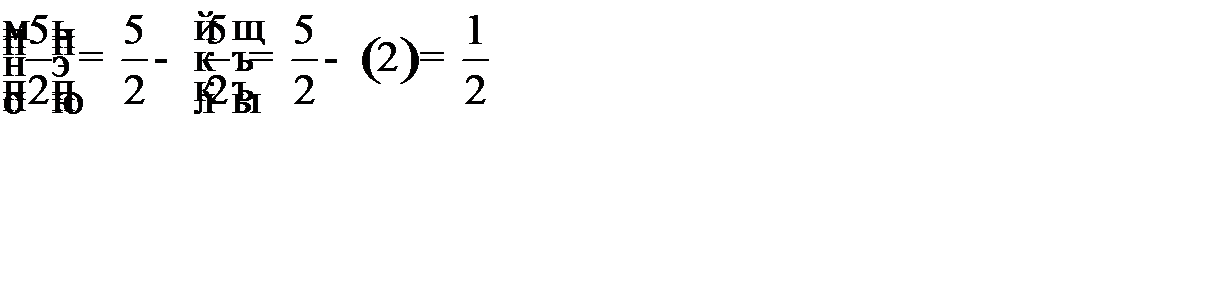. Правильное отсечение принимает вид:

. Преобразуем полученное неравенство в эквивалентное уравнение, вводя неотрицательную переменную , - целое.

(4.3)

На основе таблицы 4.4 составляем таблицу 4.5 путем присоединения строки для уравнения (4.3).

Таблица 4.5

БП		СП
- -

Решаем расширенную задачу симплексным методом. Содержащийся в таблице 4.5 план не является опорным, так как в столбце свободных членов имеется отрицательный элемент . Поэтому, прежде всего, необходимо найти опорный план. Для этого выберем за разрешающий столбец первый. Найдем в этом столбце минимальное симплексное отношение: Оно соответствует третьей строке, которая и будет разрешающей. Разрешающий элемент - . Выполнив симплексные преобразования, придем к таблице 4.6, в которой план не является оптимальным поскольку в индексной строке имеется отрицательный элемент .Столбец, содержащий этот отрицательный элементбудет разрешающим.

Таблица 4.6

БП		СП
		-1 2
		-2

Найдем в этом столбце минимальное симплексное отношение которое соответствует третьей строке. Эта строка и будет разрешающей.

Выполнив симплексное преобразование с элементом «1», приходим к таблице 4.7,

Таблица 4.7

БП		СП

в которой опорный план оказался и оптимальным, и целочисленным.

Таким образом, оптимальным будет вариант, при котором приобретается 3 машины типа А и 1 машина типа В. При этом все денежные средства будут израсходованы , но 1 м производственной площади останется неиспользованным .Максимальная производительность за смену при этом будет равна 21единице изделий.

Лекция 5 Экономико-математические методы и модели оптимального планирования в промышленности, АПК (продолжение)

Вопросы, изучаемые на лекции:

5.1. Математическая модель транспортной задачи

5.2. Признак разрешимости транспортной модели

5.3. Построение начального опорного плана

5.4. Метод потенциалов построения оптимального опорного плана