Признак разрешимости транспортной модели
Теорема 5.1. Для того чтобы транспортная модель имела допустимые планы, необходимо и достаточно выполнения равенства:
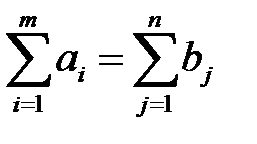 .
.
Доказательство.Необходимость. Пусть система (5.2) и (5.3) совместимы, тогда, сложив элементы матрицы 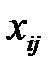 по строкам, получим
по строкам, получим 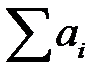 . Если сложить те же элементы по столбцам, то получим
. Если сложить те же элементы по столбцам, то получим 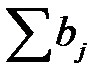 . Но от переменных мест слагаемых сумма не меняется. Поэтому
. Но от переменных мест слагаемых сумма не меняется. Поэтому 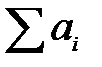 =
= 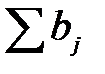 .
.
Достаточность. Пусть 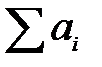 =
= 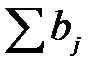 = А. Рассмотрим числа (эти числа рассматриваются произвольного вида)
= А. Рассмотрим числа (эти числа рассматриваются произвольного вида) 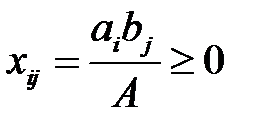 . Нам нужно доказать, что существуют положительные числа, которые определяют допустимый план.
. Нам нужно доказать, что существуют положительные числа, которые определяют допустимый план.
Они удовлетворяют всем ограничениям задачи. Действительно, просуммировав по i:
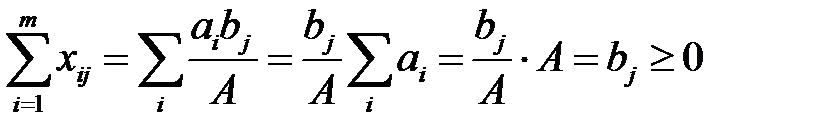 ,
,
просуммировав по j:
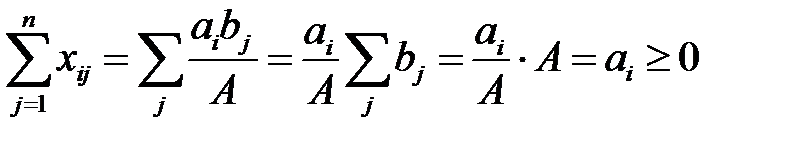
Таким образом, допустимый план существует. Теорема доказана.
Если модель транспортной задачи открытая, т. е. если:
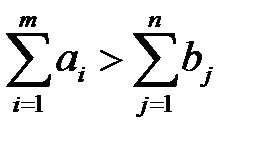 или
или 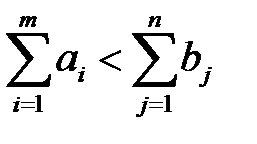 ,
,
то ее можно преобразовать в закрытую. В случае если запасы поставщиков больше потребностей получателей 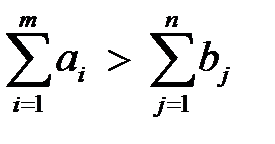 , то в математическую модель вводится фиктивный (n + 1)-й пункт назначения (потребитель), запросы которого равны излишку запаса:
, то в математическую модель вводится фиктивный (n + 1)-й пункт назначения (потребитель), запросы которого равны излишку запаса:
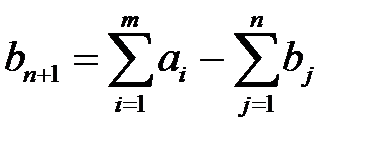 .
.
Тарифы 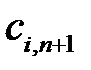 на доставку груза в этот пункт назначения будем считать равными нулю. Получим расширенную закрытую задачу. Ее оптимальный план даст оптимальный план исходной задачи. Поставки
на доставку груза в этот пункт назначения будем считать равными нулю. Получим расширенную закрытую задачу. Ее оптимальный план даст оптимальный план исходной задачи. Поставки 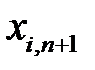 в оптимальном плане расширенной задачи покажут остатки продукции на складах поставщиков.
в оптимальном плане расширенной задачи покажут остатки продукции на складах поставщиков.
Если потребности превышают запасы 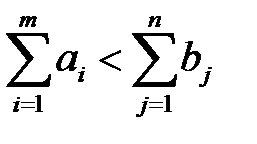 , то вводят (
, то вводят ( 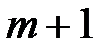 )-го фиктивного поставщика. Его запасы считают равными недостающей продукции:
)-го фиктивного поставщика. Его запасы считают равными недостающей продукции: 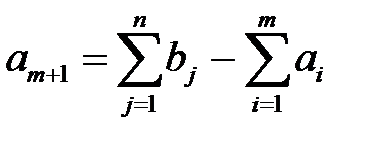
Тарифы 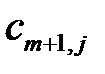 на доставку продуктов от этого фиктивного поставщика полагаем равными нулю. Поставки
на доставку продуктов от этого фиктивного поставщика полагаем равными нулю. Поставки 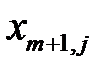 в оптимальном плане расширенной задачи покажут объемы недостачи продукции.
в оптимальном плане расширенной задачи покажут объемы недостачи продукции.
Построение начального опорного плана
Рассмотрим матрицу системы ограничений (5.2)-(5.3) транспортной модели:

Специфика матрицы системы ограничений состоит в следующем:
1) коэффициенты при неизвестных во всех ограничениях равны 1;
2) каждая неизвестная величина встречается только в двух уравнениях: раз в системе (5.2), раз в системе (5.3);
3) система уравнений симметрична относительно всех переменных 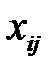 .
.
Для транспортной модели важное значение имеет следующая теорема.
Теорема 5.2. Ранг матрицы транспортной модели на единицу меньше числа уравнений: 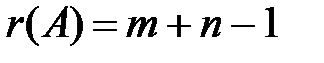 .
.
Из теоремы 5.2 следует, что каждый опорный план должен иметь mn – (m + n – 1) = (m – 1)(n – 1) свободных переменных, равных нулю, и m + n – 1 базисных переменных.
Отметим, что:
1) допустимый план транспортной модели является опорным тогда и только тогда, когда из занятых этим планом клеток нельзя образовать ни одного замкнутого цикла;
2) если имеем опорный план, то для каждой свободной клетки можно образовать и притом только один замкнутый цикл, содержащий данную клетку и некоторую часть занятых клеток.
Назовем замкнутым циклом непрерывную замкнутую ломаную линию, вершины которой находятся в клетках матрицы, а звенья расположены вдоль строк и столбцов, при этом каждое звено соединяет две клетки цикла, одно из них располагается по строке, а другое по столбцу.
Примеры циклов:
План перевозок транспортной модели будем отыскивать непосредственно в распределительной таблице. Причем, если переменная 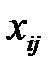 принимает значение
принимает значение 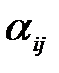 ≠ 0, то в соответствующую клетку (i, j) будем записывать это значение, если же
≠ 0, то в соответствующую клетку (i, j) будем записывать это значение, если же 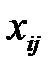 = 0, то клетку (i, j) оставим свободной. Тогда, в силу теоремы 5.2, опорный план должен содержать m + n – 1 занятых клеток, а остальные будут свободные. Заполненные клетки соответствуют базисным неизвестным, а незанятые – свободным неизвестным.
= 0, то клетку (i, j) оставим свободной. Тогда, в силу теоремы 5.2, опорный план должен содержать m + n – 1 занятых клеток, а остальные будут свободные. Заполненные клетки соответствуют базисным неизвестным, а незанятые – свободным неизвестным.
Существуют следующие способы построения начального опорного плана: 1) правило «северо-западного угла»; 2) правило «минимального элемента»; 3) метод Фогеля.
Рассмотрим правило «минимального элемента».
Сущность этого правила состоит в том, что на каждом шаге осуществляется максимально возможное «перемещение» продукции в клетку с минимальным тарифом 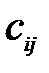 . Поэтому просматриваются тарифы в таблице 5.1 и в первую очередь заполняется клетка с минимальным тарифом:
. Поэтому просматриваются тарифы в таблице 5.1 и в первую очередь заполняется клетка с минимальным тарифом: 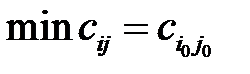 . В эту клетку с наименьшим тарифом записывается меньшее из чисел
. В эту клетку с наименьшим тарифом записывается меньшее из чисел 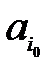 и
и 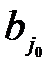 . Если
. Если 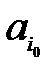 >
> 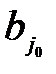 , то
, то 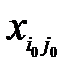 =
= 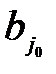 и из рассмотрения исключается столбец
и из рассмотрения исключается столбец 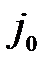 . Запасы поставщика
. Запасы поставщика 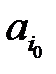 корректируем, т. е. считаем их равными
корректируем, т. е. считаем их равными
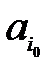 –
– 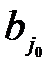 . Если же
. Если же 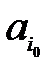 =
= 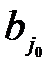 , то вычеркиваем строку
, то вычеркиваем строку 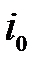 и столбец
и столбец 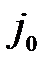 ( в случае
( в случае 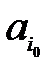 =
= 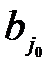 опорный план оказывается вырожденным). Вычеркнув один из рядов таблицы и скорректировав запасы поставщика либо потребности получателя на величину поставки
опорный план оказывается вырожденным). Вычеркнув один из рядов таблицы и скорректировав запасы поставщика либо потребности получателя на величину поставки 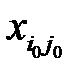 с оставшейся таблицей меньшего размера, поступаем аналогично предыдущему. Процесс распределения продукции заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей удовлетворен. В результате должно быть заполнено
с оставшейся таблицей меньшего размера, поступаем аналогично предыдущему. Процесс распределения продукции заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей удовлетворен. В результате должно быть заполнено 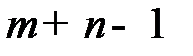 клеток распределительной таблицы. Если число заполненных клеток меньше чем m + n – 1, то в клетку с наименьшим тарифом, среди свободных клеток, вводится базисный нуль и клетка считается заполненной. Клетка для базисного нуля выбирается таким образом, чтобы из заполненных клеток нельзя было составить замкнутый цикл.
клеток распределительной таблицы. Если число заполненных клеток меньше чем m + n – 1, то в клетку с наименьшим тарифом, среди свободных клеток, вводится базисный нуль и клетка считается заполненной. Клетка для базисного нуля выбирается таким образом, чтобы из заполненных клеток нельзя было составить замкнутый цикл.
Метод потенциалов построения оптимального опорного плана
После того, как построен начальный опорный план, нужно определить, является ли он оптимальным. Для определения оптимальности плана пользуются следующей теоремой:
Теорема 5.3.Если план 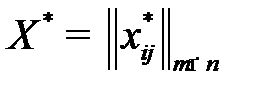 транспортной модели является оптимальным, то ему соответствует система из
транспортной модели является оптимальным, то ему соответствует система из 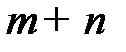 чисел
чисел 
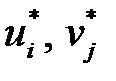 , удовлетворяющих условиям
, удовлетворяющих условиям 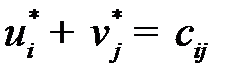 для
для 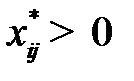 и
и 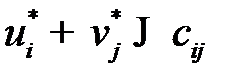 для
для 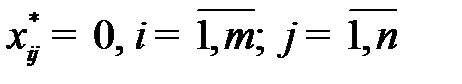 .
.
Числа 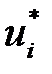 и
и 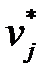 называются потенциалами
называются потенциалами 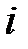 -го поставщика и
-го поставщика и  -го потребителя.
-го потребителя.
Из этой теоремы следует, что для оптимального плана транспортной модели каждой заполненной клетке в распределительной таблице соответствует сумма потенциалов, равная тарифу этой клетки, а каждой свободной клетке соответствует сумма потенциалов, не превышающая тарифа этой клетки.
В соответствии с теоремой 5.3 каждому поставщику (каждой строке) ставим в соответствие некоторое число 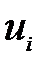 (
( 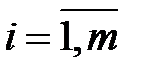 ) называемое потенциалом поставщика
) называемое потенциалом поставщика 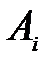 , а каждому потребителю (каждому столбцу) – некоторое число
, а каждому потребителю (каждому столбцу) – некоторое число 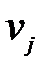 , называемое потенциалом потребителя
, называемое потенциалом потребителя 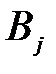 (
( 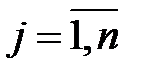 ).
).
Числа 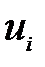 и
и 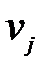 выбирают так, чтобы в любой загруженной клетке сумма их равнялась тарифу этой клетки.
выбирают так, чтобы в любой загруженной клетке сумма их равнялась тарифу этой клетки.
Так как количество всех чисел 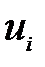 и
и 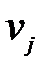 составляет m + n, а занятых клеток m + n – 1, то для определения чисел
составляет m + n, а занятых клеток m + n – 1, то для определения чисел 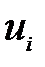 и
и 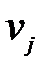 решается система из m + n – 1 уравнений:
решается система из m + n – 1 уравнений: 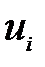 +
+ 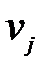 =
= 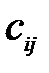 , с m + n неизвестными. Придав одному неизвестному произвольное значение (например,
, с m + n неизвестными. Придав одному неизвестному произвольное значение (например, 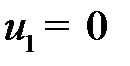 ), находим однозначные значения остальных неизвестных.
), находим однозначные значения остальных неизвестных.
Затем определяем. оценки свободных клеток 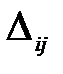 =
= 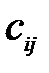 –(
–( 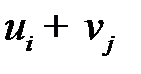 )– разность между тарифом клетки и суммой соответствующих потенциалов поставщиков и потребителей. План оптимален тогда, когда для каждой свободной клетки (если
)– разность между тарифом клетки и суммой соответствующих потенциалов поставщиков и потребителей. План оптимален тогда, когда для каждой свободной клетки (если 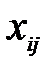 = 0) ее оценка не отрицательна, т.е.
= 0) ее оценка не отрицательна, т.е. 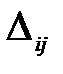 =
= 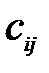 – (
– ( 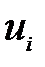 +
+ 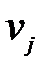 ) ≥ 0 (если
) ≥ 0 (если 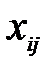 = 0).
= 0).
Если оценки свободных клеток отрицательны, то это указывает на перспективность клеток, загрузка которых приведет к улучшению плана (положительные и нулевые оценки исключают возможность улучшения плана). Для наиболее перспективной клетки (с наименьшей оценкой) строится замкнутый цикл, вершинам которого приписываются чередующие знаки (свободной клетке приписывается положительный знак). В клетках, соответствующих отрицательным вершинам, отыскивается наименьший груз, который и перемещается по клеткам замкнутого цикла, т. е. прибавляется к поставкам 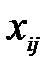 в клетках со знаком плюс (включая свободную) и вычитается в клетках со знаком минус.
в клетках со знаком плюс (включая свободную) и вычитается в клетках со знаком минус.
В новом плане вновь определяются потенциалы строк и столбцов и вычисляются оценки свободных клеток. Когда среди оценок не окажется больше отрицательных, полученный план будет оптимальным.
Алгоритм метода потенциалов имеет вид:
1) построить опорный план перевозок по одному из правил;
2) вычислить потенциалы  и
и 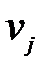 соответственно поставщиков и потребителей, решив систему уравнений вида
соответственно поставщиков и потребителей, решив систему уравнений вида 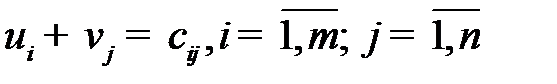 ;
;
3) определить оценки 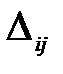 =
= 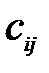 – (
– ( 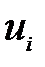 +
+ 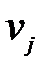 ) для свободных клеток;
) для свободных клеток;
4) если все 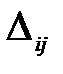 ≥ 0, то план оптимальный;
≥ 0, то план оптимальный;
5) если существуют отрицательные оценки свободных клеток, то план не оптимален. Находим наименьшую из отрицательных оценок: 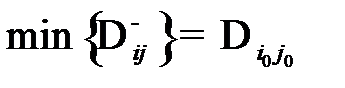 ;
;
6) клетка ( 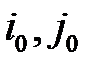 ), для которой оценка
), для которой оценка 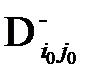 наименьшая отмечается знаком
наименьшая отмечается знаком 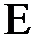 . Она называется перспективной.
. Она называется перспективной.
7) Строится цикл пересчета. Из клеток отрицательного полуцикла вычитаем значение θ, а к перевозкам клеток положительного полуцикла прибавляем 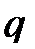 :
: 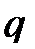 =
= 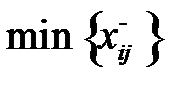 ,
, 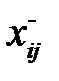 – наименьшее значение поставки в вершинах отрицательного полуцикла. Клетки, которые не находятся в вершинах цикла, остаются без изменения. В общем виде переход к новому опорному плану осуществляется по формуле:
– наименьшее значение поставки в вершинах отрицательного полуцикла. Клетки, которые не находятся в вершинах цикла, остаются без изменения. В общем виде переход к новому опорному плану осуществляется по формуле:
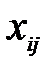 – для клеток, не входящих в цикл;
– для клеток, не входящих в цикл;
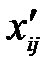 =
= 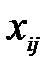 + θ – для клеток положительного полуцикла;
+ θ – для клеток положительного полуцикла;
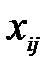 – θ – для клеток отрицательного полуцикла.
– θ – для клеток отрицательного полуцикла.
и т.д. до получения неотрицательных оценок 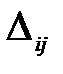 ≥ 0 всех свободных клеток.
≥ 0 всех свободных клеток.
Пример 5.1. Решить транспортную задачу методом потенциалов. Данные приведены в таблице 5.2.
Требуется составить план перевозок  так, чтобы минимизировать транспортные затраты.
так, чтобы минимизировать транспортные затраты.
Решение. Найдем план перевозок, не составляя математической модели. Начальный опорный план будем строить в распределительной таблице по наименьшему тарифу. Наименьший тариф 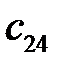 = 1 соответствует клетке (2; 4). Поместим в эту клетку наименьшее количество груза – 150. Исключаем из дальнейшего рассмотрения четвертый столбец, соответствующий потребителю
= 1 соответствует клетке (2; 4). Поместим в эту клетку наименьшее количество груза – 150. Исключаем из дальнейшего рассмотрения четвертый столбец, соответствующий потребителю 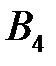 , спрос которого полностью удовлетворен, и вторую строку, поскольку вся продукция второго производителя вывезена.
, спрос которого полностью удовлетворен, и вторую строку, поскольку вся продукция второго производителя вывезена.
Таблица 5.2
Поставщики 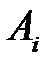
| Потребители В 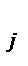
| |||||
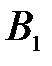 (100) (100)
| 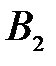 (120) (120)
| 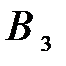 (130) (130)
| 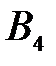 (150) (150)
| |||
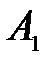 (200) (200)
| – | + | ||||
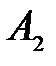 (150) (150)
| + |

| ||||
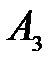 (150) (150)
|

|
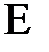
| ||||
Наименьший тариф оставшейся части 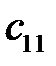 = 4 и
= 4 и 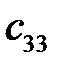 = 4 для двух клеток (1; 1) и (3; 3). Выбираем клетку (1; 1), в которую помещаем количество груза
= 4 для двух клеток (1; 1) и (3; 3). Выбираем клетку (1; 1), в которую помещаем количество груза 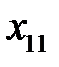 = 100 единиц и исключаем из рассмотрения первый столбец, так как потребность в грузе удовлетворена полностью. В оставшейся части таблицы минимальный тариф
= 100 единиц и исключаем из рассмотрения первый столбец, так как потребность в грузе удовлетворена полностью. В оставшейся части таблицы минимальный тариф 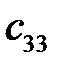 = 4. В клетку (3; 3) помещаем
= 4. В клетку (3; 3) помещаем 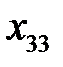 = 130 единиц и исключаем из рассмотрения третий столбец. Остался второй столбец. У поставщика
= 130 единиц и исключаем из рассмотрения третий столбец. Остался второй столбец. У поставщика 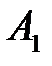 остался груз 100 единиц, у
остался груз 100 единиц, у 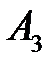 – 20 единиц. Помещаем их в клетки (1; 2) и (3; 2) соответственно.
– 20 единиц. Помещаем их в клетки (1; 2) и (3; 2) соответственно.
Так как при построении опорного плана занятых клеток 5 < m + n – 1 = 6, то в свободную клетку, которой соответствует наименьший тариф, заносится «базисный» нуль и эта клетка считается занятой. Таким образом, получили 6 заполненных клеток, которые не образуют цикла. Следовательно, план опорный.
Определяем потенциалы 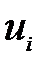 и
и 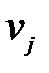 , решив систему
, решив систему 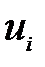 +
+ 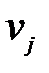 =
=  для загруженных клеток:
для загруженных клеток: 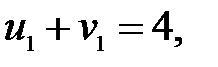
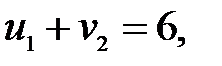
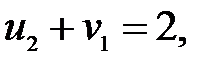
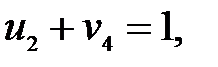
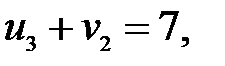
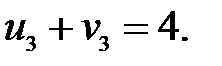
Пусть 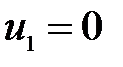 , тогда
, тогда 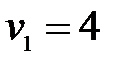 ,
, 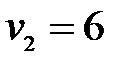 ,
, 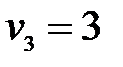 ,
, 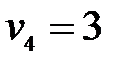 ,
, 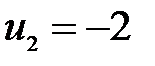 ,
, 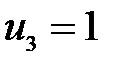 . Определяем косвенные тарифы для свободных клеток:
. Определяем косвенные тарифы для свободных клеток:
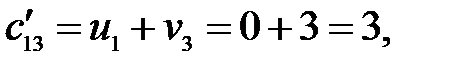
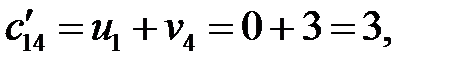
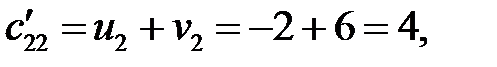
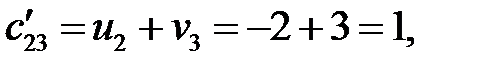
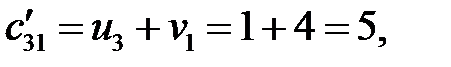
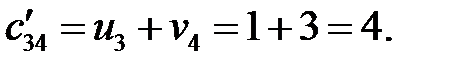
Находим оценки свободных клеток 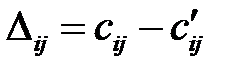 :
:
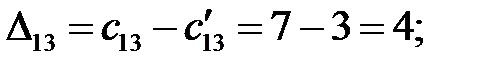
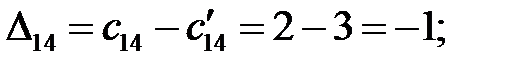
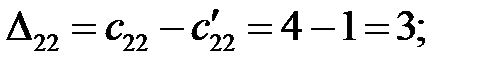
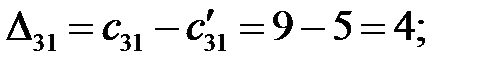
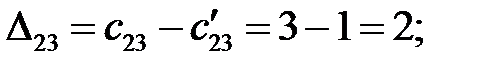
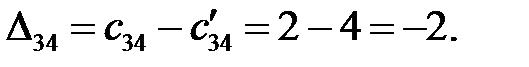
Построенный план перевозок не является оптимальным, так как среди оценок свободных клеток имеются отрицательные, 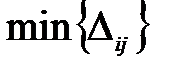 =
= 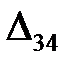 = –2. Клетку (3; 4) отмечаем знаком
= –2. Клетку (3; 4) отмечаем знаком  . Она называется перспективной.
. Она называется перспективной.
Для свободной клетки (3; 4) строим замкнутый цикл, который включает клетки: (3; 4), (3; 2), (1; 2), (1; 1), (2; 1), (2; 4), (3; 4). Их m + n = 3 + 4 = 7. Свободной клетке приписывается знак «+», в следующей (по часовой или против часовой стрелки) – «минус», в следующей «плюс» и т.д. Знаки вершин цикла чередуются. В отрицательных вершинах цикла выбираем наименьшее значение поставки θ =  = min{150, 100, 20} = 20 (в клетках отрицательного полуцикла). Соответствующая клетка выводится из числа заполненных клеток. Чтобы общий баланс цикла не изменился из клеток отрицательного полуцикла, вычитаем значение θ = 20, а к перевозкам клеток положительного полуцикла прибавляем θ = 20. Эта операция называется сдвигом по циклу на величину θ.
= min{150, 100, 20} = 20 (в клетках отрицательного полуцикла). Соответствующая клетка выводится из числа заполненных клеток. Чтобы общий баланс цикла не изменился из клеток отрицательного полуцикла, вычитаем значение θ = 20, а к перевозкам клеток положительного полуцикла прибавляем θ = 20. Эта операция называется сдвигом по циклу на величину θ.
Клетки, которые не находятся в вершинах цикла, остаются без изменения. Процесс сдвига по циклу меняет план, но план остается опорным. Действительно, цикл, по которому производится сдвиг, содержит в каждом ряде только по две вершины. Баланс не нарушается. После сдвига клетка отрицательного полуцикла с минимальной перевозкой исключается из числа заполненных, а в перспективной клетке, включенной в набор, окажется θ = =20. Всего заполненных клеток остается m + n – 1. Новый план будет ацикличным, так как единственный цикл нарушается исключением клетки (3; 2). Полученный план – опорный. Переход к новому опорному плану осуществляется по формуле:
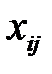 – для клеток, не входящих в цикл;
– для клеток, не входящих в цикл;
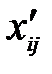 =
= 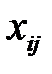 + θ – для клеток положительного полуцикла;
+ θ – для клеток положительного полуцикла;
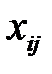 – θ – для клеток отрицательного полуцикла.
– θ – для клеток отрицательного полуцикла.
Для опорного плана 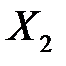 составляем таблицу 5.3.
составляем таблицу 5.3.
Таблица 5.3
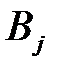  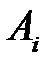
| 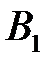 (100) (100)
| 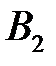 (120) (120)
| 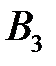 (130) (130)
| 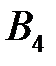 (150) (150)
| 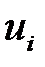
|
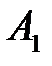 (200) (200)
|

|

| 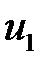 = 0 = 0
| ||
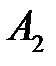 (150) (150)
| 20 + |

| 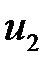 = –2 = –2
| ||
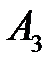 (150) (150)
| 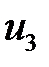 = –1 = –1
| ||||
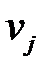
| 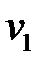 = 4 = 4
| 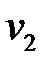 = 6 = 6
| 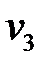 = 5 = 5
| 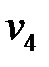 = 4 = 4
|
Определяем потенциалы для загруженных клеток:
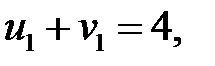
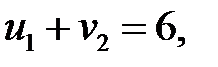
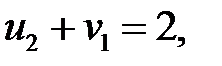
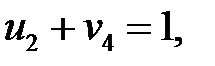
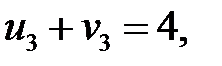
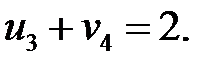
Пусть 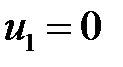 , тогда
, тогда 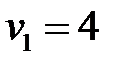 ,
, 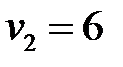 ,
, 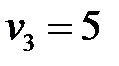 ,
, 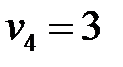 ,
, 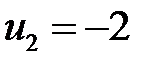 ,
, 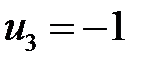 .
.
Находим оценки свободных клеток:
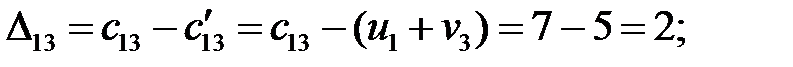
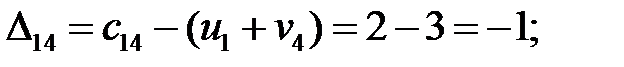
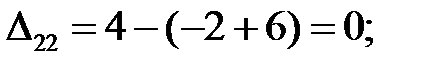
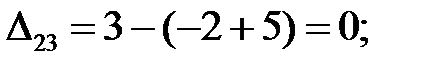
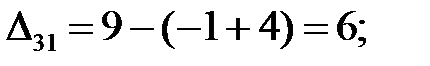
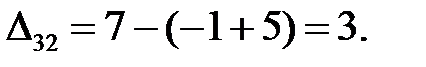
Построенный план не является оптимальным, так как среди оценок есть отрицательные: ∆  = –1.
= –1.
Условие оптимальности нарушается в клетке (1; 4). Клетку (1; 4) отмечаем знаком  . Она называется перспективной. Включаем ее в набор заполненных. Строим цикл пересчета: (1; 4), (2; 4), (2; 1), (1; 1), (1; 4) и делаем сдвиг по циклу на величину поставки: θ =
. Она называется перспективной. Включаем ее в набор заполненных. Строим цикл пересчета: (1; 4), (2; 4), (2; 1), (1; 1), (1; 4) и делаем сдвиг по циклу на величину поставки: θ =  = min{80, 130}= 80.
= min{80, 130}= 80.
Для опорного плана 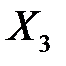 составляем таблицу 5.4.
составляем таблицу 5.4.
Таблица 5.4
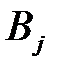
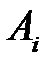
| 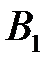 (100) (100)
| 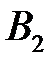 (120) (120)
| 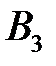 (130) (130)
| 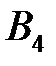 (150) (150)
| 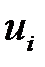
|
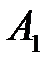 (200) (200)
|

| + | |||
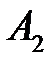 (150) (150)
|

|

| -1 | ||
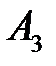 (150) (150)
| |||||
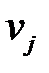
|
Для опорного плана 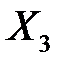 определяем потенциалы для загруженных клеток, решив систему:
определяем потенциалы для загруженных клеток, решив систему:
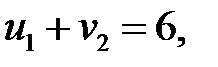
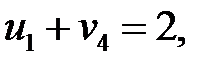
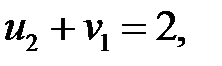
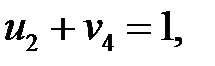
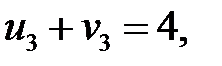
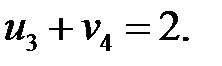
Пусть 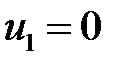 , тогда
, тогда 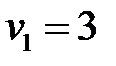 ,
, 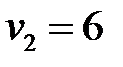 ,
, 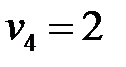 ,
, 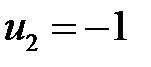 ,
, 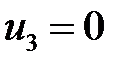 ,
, 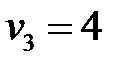 .
.
Находим оценки свободных клеток:
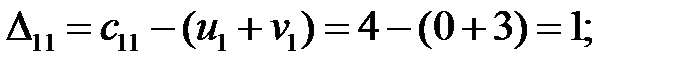
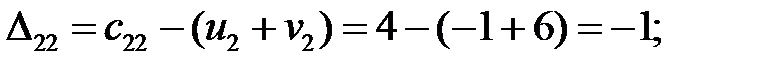
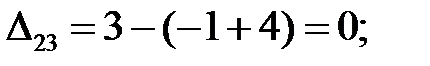
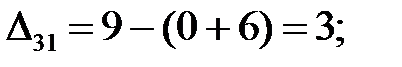
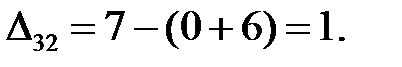
Условие оптимальности нарушается в клетке (2; 2) . так как ∆  = –1. Строим цикл пересчета (2; 2), (1; 2), (1; 4), (2; 4), (2; 2) и сделаем сдвиг по циклу на величину поставки: θ =
= –1. Строим цикл пересчета (2; 2), (1; 2), (1; 4), (2; 4), (2; 2) и сделаем сдвиг по циклу на величину поставки: θ =  = min{120, 50} = 50.
= min{120, 50} = 50.
Для опорного плана 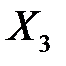 составляем таблицу 5.5.
составляем таблицу 5.5.
Таблица 5.5
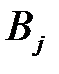
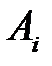
| 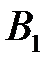 (100) (100)
| 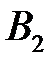 (120) (120)
| 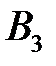 (130) (130)
| 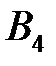 (150) (150)
| 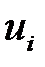
|
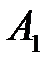 (200) (200)
| 4

| – | |||
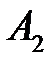 (150) (150)
|
 100
100
| + | –2 | ||
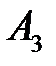 (150) (150)
| |||||
|
Для опорного плана Х 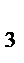 определяем потенциалы для загруженных клеток:
определяем потенциалы для загруженных клеток:
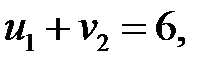
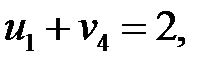
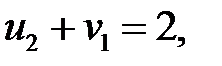
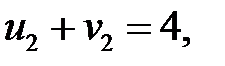
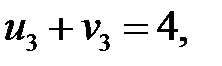
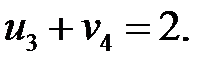
Пусть 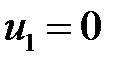 , тогда
, тогда 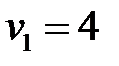 ,
, 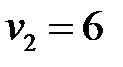 ,
, 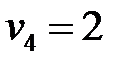 ,
, 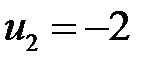 ,
, 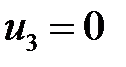 ,
, 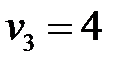 .
.
Находим оценки свободных клеток:
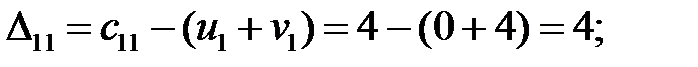
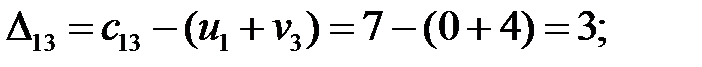
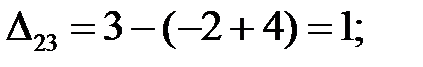
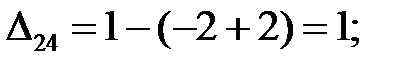
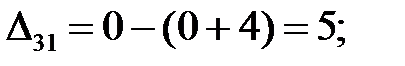
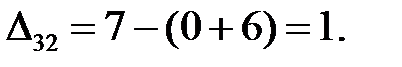
Полученный план перевозок
 является оптимальным, так как все оценки свободных клеток неотрицательны, т. е.
является оптимальным, так как все оценки свободных клеток неотрицательны, т. е. 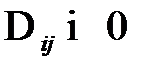 . Но так как
. Но так как 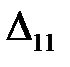 = 0, то этот план не единственный оптимальный.
= 0, то этот план не единственный оптимальный.
Замечания: 1.Многие задачи экономики:
· об оптимальном распределении производства изделий между предприятиями;
· о рациональном закреплении механизмов за определенными видами работ;
· об оптимальном использовании транспорта;
· об оптимальном распределении посевных площадей;
· об оптимальных назначениях и др.
не являются транспортными в физическом смысле, хотя в математическом отношении, подобны транспортным задачам. Поэтому для их решения можно использовать метод потенциалов.
2.Если в задачах транспортного типа определяется максимум целевой функции, то при составлении начального опорного плана в первую очередь заполняются клетки с наиболее высокими значениями показателя критерия оптимальности. Выбор клетки, подлежащей заполнению при переходе от одного опорного плана к другому, производится по положительной оценке. Оптимальным будет опорный план, для которого оценки свободных клеток неположительны (  ).
).
Дата добавления: 2015-09-29; просмотров: 1178;
