Модели матричных игр со смешанными стратегиями игроков. Свойства смешанных стратегий
Рассмотрим матричную игру:
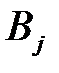
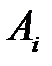
| 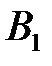
| 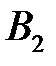
| … | 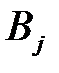
| … | 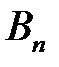
| 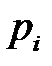
|
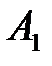
| 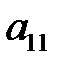
| 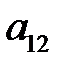
| … | 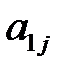
| 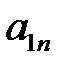
| 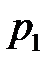
| |
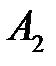
| 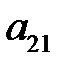
| 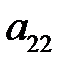
| … | 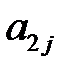
| … | 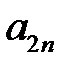
| 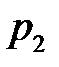
|
| … | … | … | … | … | … | … | … |
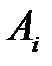
| 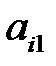
| 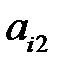
| … | 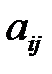
| … | 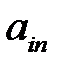
| 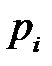
|
| … | … | … | … | … | … | … | … |
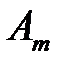
| 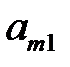
| 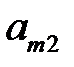
| … | 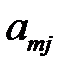
| … | 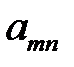
| 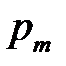
|
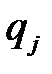
| 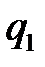
| 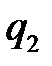
| … | 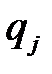
| … | 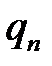
|
Обозначим через 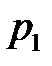 ,…,
,…, 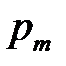 вероятности, с которыми игрок А использует чистые стратегии
вероятности, с которыми игрок А использует чистые стратегии 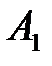 , …,
, …, 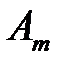 . В силу свойств вероятностей:
. В силу свойств вероятностей:
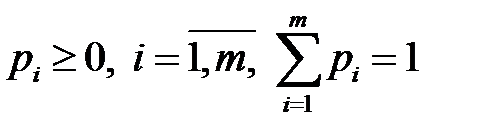 . (6.3)
. (6.3)
Упорядоченное множество р = ( 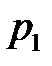 , …,
, …, 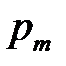 ), элементы которого удовлетворяют условиям (6.3), полностью определяют характер игры игрока А и называется его смешанной стратегией. Итак, смешанной стратегией игрока А является полный набор вероятностей применения его чистых стратегий. Множество смешанных стратегий определяется случайным выбором чистых стратегий. Любая его чистая стратегия А
), элементы которого удовлетворяют условиям (6.3), полностью определяют характер игры игрока А и называется его смешанной стратегией. Итак, смешанной стратегией игрока А является полный набор вероятностей применения его чистых стратегий. Множество смешанных стратегий определяется случайным выбором чистых стратегий. Любая его чистая стратегия А 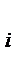 может рассматриваться как частный случай смешанной стратегии, i-я компонента которой равна 1, а остальные равны нулю: р = (0; …; 1; …; 0).
может рассматриваться как частный случай смешанной стратегии, i-я компонента которой равна 1, а остальные равны нулю: р = (0; …; 1; …; 0).
Упорядоченное множество q = ( 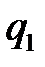 , …,
, …, 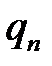 ), элементы которого удовлетворяют соотношениям
), элементы которого удовлетворяют соотношениям 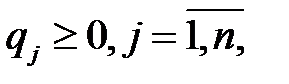
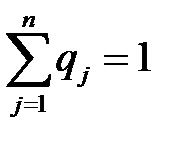 , называются смешанной стратегией игрока В.
, называются смешанной стратегией игрока В.
Применение смешанных стратегий p и q игроками А и В означает, что игрок А использует стратегию 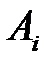 с вероятностью
с вероятностью 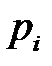 , а игрок В – стратегию
, а игрок В – стратегию 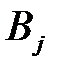 с вероятностью
с вероятностью 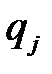 . Поскольку игроки выбирают свои стратегии случайно и независимо друг от друга, то вероятность выбора комбинации стратегий (
. Поскольку игроки выбирают свои стратегии случайно и независимо друг от друга, то вероятность выбора комбинации стратегий ( 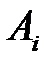 ,
, 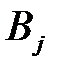 ) будет равна
) будет равна 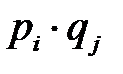 . При использовании смешанных стратегий игра приобретает случайный характер, поэтому случайными будут и выигрыши игрока А и проигрыши игрока В. Следовательно, можно вести речь лишь о средней величине (математическом ожидании) выигрыша (проигрыша). Эта величина является функцией смешанных стратегий p и q и определяется по формуле:
. При использовании смешанных стратегий игра приобретает случайный характер, поэтому случайными будут и выигрыши игрока А и проигрыши игрока В. Следовательно, можно вести речь лишь о средней величине (математическом ожидании) выигрыша (проигрыша). Эта величина является функцией смешанных стратегий p и q и определяется по формуле:
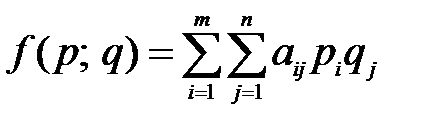 .
.
Функция f(p; q) называется платежной функцией игры с матрицей 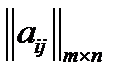 .
.
Смешанные стратегии 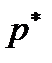 ,
, 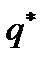 назовем оптимальными смешанными стратегиями игроков А и В, если они удовлетворяют неравенству:
назовем оптимальными смешанными стратегиями игроков А и В, если они удовлетворяют неравенству:
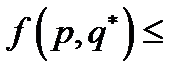
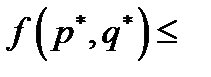
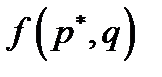 (6.4)
(6.4)
для любых стратегий 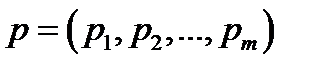 и
и 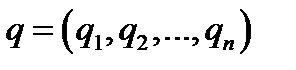 .
.
Значение 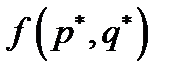 платежной функции при оптимальных стратегиях определяет цену игры v, т. е.
платежной функции при оптимальных стратегиях определяет цену игры v, т. е. 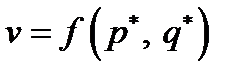 .
.
В седловой точке 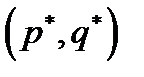 платежная функция
платежная функция 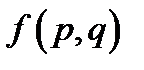 достигает максимума по смешанным стратегиям
достигает максимума по смешанным стратегиям 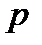 игрока
игрока 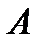 и минимума по смешанным стратегиям
и минимума по смешанным стратегиям 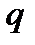 игрока
игрока 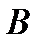 .
.
Рассмотрим игру с матрицей 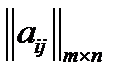 и предположим, что
и предположим, что 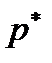 и
и 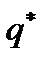 – оптимальные смешанные стратегии игроков и
– оптимальные смешанные стратегии игроков и 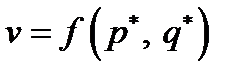 – цена игры. Проверку того, что набор
– цена игры. Проверку того, что набор 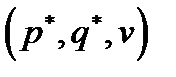 является решением, можно провести при помощи теоремы 6.2.
является решением, можно провести при помощи теоремы 6.2.
Теорема 6.2. Для того, чтобы смешанные стратегии 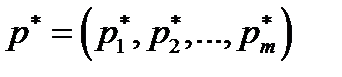 и
и 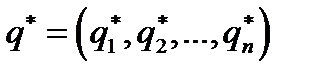 , были оптимальными для игроков А и В в игре с матрицей
, были оптимальными для игроков А и В в игре с матрицей 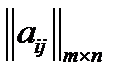 и ценой v, необходимо и достаточно выполнения неравенств:
и ценой v, необходимо и достаточно выполнения неравенств:
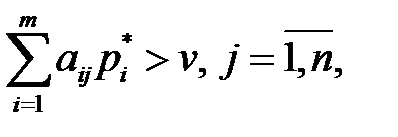
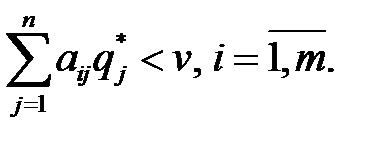
Кроме того, смешенные стратегии удовлетворяют еще следующим теоремам.
Теорема 6.3. В смешанных стратегиях любая конечная матричная игра имеет седловую точку.
Теорема 6.4. Если один из игроков придерживается своей оптимальной смешанной стратегии, то его выигрыш остается неизменным и равным цене игры независимо от того, какую стратегию применяет другой игрок, если только тот не выходит за пределы своих активных стратегий.
Активные стратегии – это чистые стратегии игрока, входящие в оптимальную смешанную стратегию с вероятностями, отличными от нуля.
Из теоремы 6.2 вытекает принципиальное решение матричной игры: надо найти неотрицательное решение ( 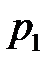 ,
, 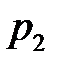 , …,
, …, 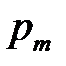 ,
, 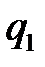 ,
, 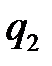 , …,
, …, 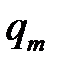 , v) системы
, v) системы 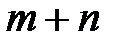 линейных неравенств и линейных уравнений:
линейных неравенств и линейных уравнений:
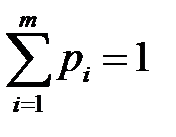 ;
; 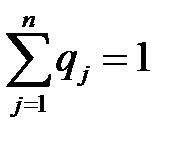 .
.
Отметим, что число активных стратегий игроков не превышает наименьшего из чисел m и n.
Решение матричной игры можно упростить, если воспользоваться доминированием одних стратегий над другими.
Говорят, что стратегия 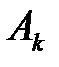 доминирует над стратегией
доминирует над стратегией 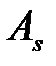 , если элементы k-й строки не меньше соответствующих элементов s-ой строки:
, если элементы k-й строки не меньше соответствующих элементов s-ой строки: 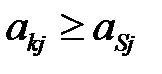 ,
, 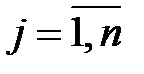 . Выигрыш игрока А в этом случае (при стратегии
. Выигрыш игрока А в этом случае (при стратегии 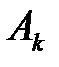 ) больше чем при стратегии
) больше чем при стратегии 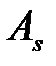 , какой бы стратегией не воспользовался игрок В. Стратегию
, какой бы стратегией не воспользовался игрок В. Стратегию 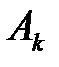 назовем доминирующей, а стратегию
назовем доминирующей, а стратегию 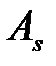 – доминируемой.
– доминируемой.
Аналогично и для столбцов:
если элементы l-го столбца не превосходят соответствующих элементов r-го столбца: 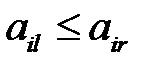 ,
, 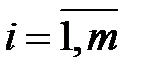 , то игроку В выгоднее применять стратегию
, то игроку В выгоднее применять стратегию 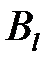 , чем
, чем 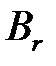 , так как он будет проигрывать меньше. Поэтому стратегия
, так как он будет проигрывать меньше. Поэтому стратегия 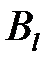 доминирует над стратегией
доминирует над стратегией 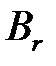 . Стратегия
. Стратегия 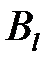 называется доминирующей, стратегия
называется доминирующей, стратегия 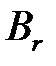 – доминируемой.
– доминируемой.
Если 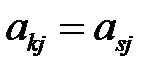 ,
, 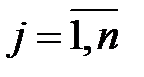 , или
, или 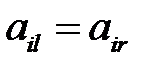 ,
, 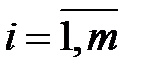 , то стратегии
, то стратегии 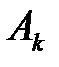 и
и 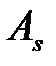 ,
, 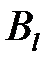 и
и 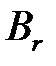 называются дублирующими.
называются дублирующими.
Пример 6.3. Выполнить возможные упрощения платежной матрицы:
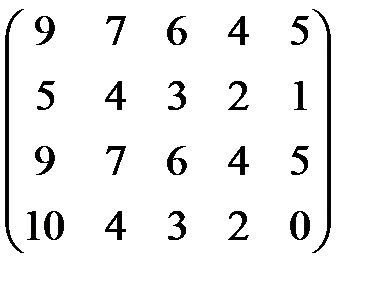
Решение. Элементы первой и третьей строки соответственно равны. Поэтому одну из них можно удалить. Элементы второй строки не превышают соответственно элементов первой строки, поэтому удаляем вторую строку и приходим к матрице
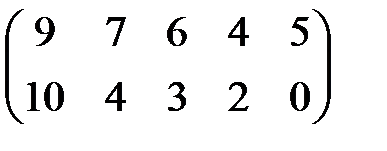
Элементы первого столбца преобразованной матрицы больше соответствующих элементов второго столбца, элементы второго столбца больше соответствующих элементов третьего столбца; элементы третьего столбца больше соответствующих элементов четвертого столбца. Поэтому доминируемые первый, второй и третий столбцы опускаем. В результате получаем матрицу
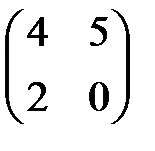 .
.
Сравнивая строки полученной матрицы, заключаем, что элементы первой строки больше соответствующих элементов второй строки. Следовательно, первая строка является доминирующей. Опуская вторую строку, получаем матрицу  , из которой следует, что наилучшей стратегией для игрока
, из которой следует, что наилучшей стратегией для игрока  является чистая стратегия
является чистая стратегия  . Опуская доминируемую стратегию
. Опуская доминируемую стратегию  игрока
игрока  , получаем матрицу
, получаем матрицу  . Итак, получили матицу, состоящую из одного элемента. Это объясняется тем, что рассматриваемая матричная игра имеет седловую точку
. Итак, получили матицу, состоящую из одного элемента. Это объясняется тем, что рассматриваемая матричная игра имеет седловую точку  , а полученный элемент 4 является седловым элементом:
, а полученный элемент 4 является седловым элементом:  . Таким образом, в результате упрощения платежной матрицы нашли решение игры:
. Таким образом, в результате упрощения платежной матрицы нашли решение игры:  . Такой же результат получим, если вместо стратегии
. Такой же результат получим, если вместо стратегии  рассмотреть стратегию
рассмотреть стратегию  , поскольку эти стратегии являются дублирующими. Следовательно, оптимальными чистыми стратегиями для игрока
, поскольку эти стратегии являются дублирующими. Следовательно, оптимальными чистыми стратегиями для игрока  являются стратегии
являются стратегии  или
или  , а для игрока
, а для игрока  - стратегия
- стратегия  , обеспечивающие наибольший выигрыш для игрока
, обеспечивающие наибольший выигрыш для игрока  , равный 4, и наименьший проигрыш игрока
, равный 4, и наименьший проигрыш игрока 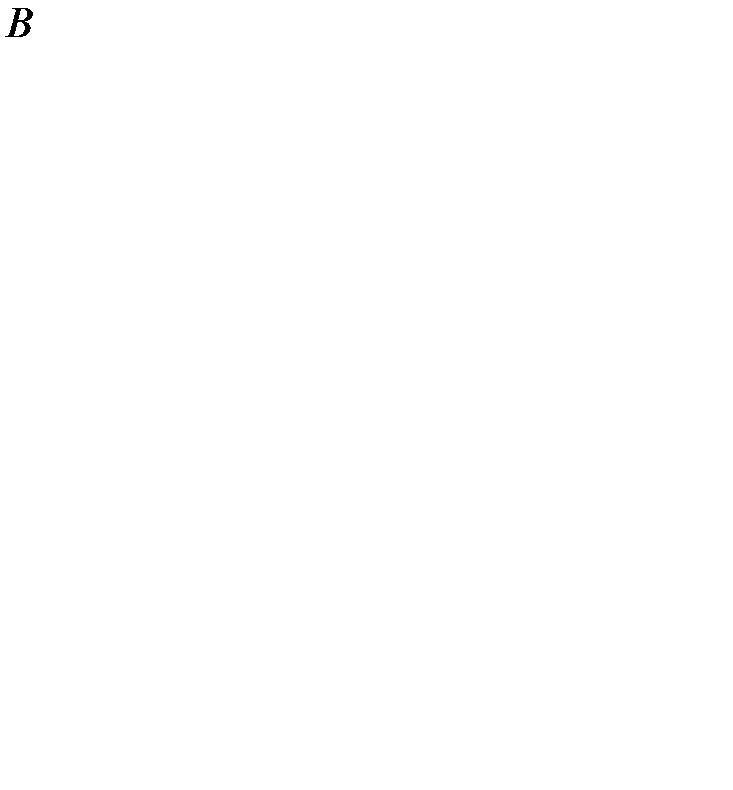 .
.
Теорема 6.5. Пусть 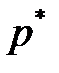 и
и 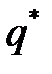 – оптимальные смешанные стратегии игроков А и В в игре I с матрицей
– оптимальные смешанные стратегии игроков А и В в игре I с матрицей 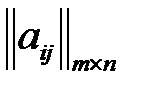 и ценой v. Тогда
и ценой v. Тогда 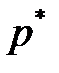 и
и 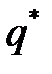 будут оптимальными и в игре I' с матрицей
будут оптимальными и в игре I' с матрицей 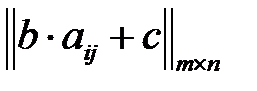 и ценой
и ценой 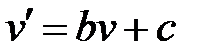 , где
, где 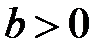 .
.
Воспользовавшись этой теоремой матрицу:
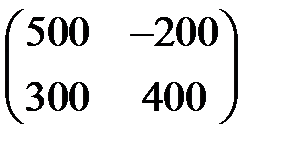
можно упростить. Сначала разделить элементы матрицы на 100, а затем прибавить к полученным значениям 2:
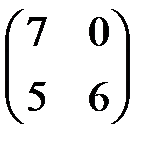
элементы последней матрицы получены по формуле:
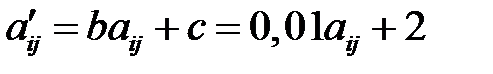 .
.
Дата добавления: 2015-09-29; просмотров: 1633;
