Решение моделей матричных игр сведением к паре взаимно двойственных линейных оптимизационных моделей
Выше установлено, что если игра имеет седловую точку, то решение ее лежит в области чистых стратегий: оптимальными будут максиминные (минимаксные) стратегии, а ценой игры – седловой элемент матрицы игры.
Оптимальные же смешанные стратегии для игр без седловых точек можно получить, решая систему 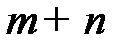 линейных неравенств:
линейных неравенств:

и линейных уравнений:
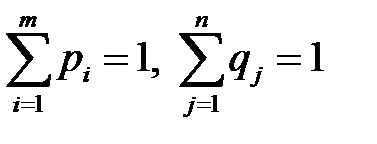 (
( 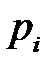 ≥ 0,
≥ 0, 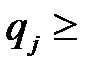 0).
0).
Этот путь нерационален, так как связан с большим объемом вычислений.
Покажем, что решение любой конечной матричной игры может быть сведено к решению линейной оптимизационной модели.
Пусть игра задана матрицей 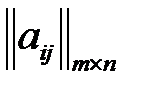 ,
, 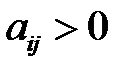 . Поскольку элементы платежной матрицы положительны, то и цена игры
. Поскольку элементы платежной матрицы положительны, то и цена игры  .
.
Найдем сначала оптимальную смешанную стратегию 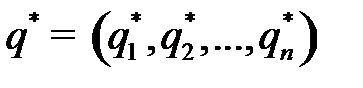 игрока В. Применяя ее, игрок В проиграет не более цены v, какую бы чистую стратегию
игрока В. Применяя ее, игрок В проиграет не более цены v, какую бы чистую стратегию 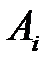 не применял игрок А, т. е.
не применял игрок А, т. е.
 .
.
Разделим обе части неравенств на v, получим:
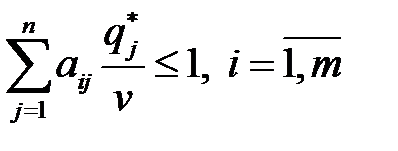 .
.
Обозначив
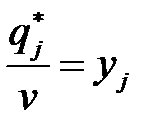 ,
, 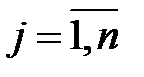 , (6.5)
, (6.5)
будем иметь:
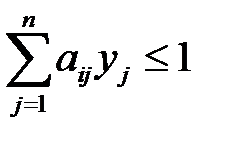 ,
, 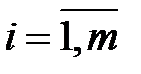 ,
,
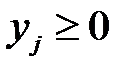 ,
, 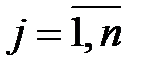 . (6.6)
. (6.6)
Кроме того, 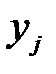 удовлетворяет условию:
удовлетворяет условию:
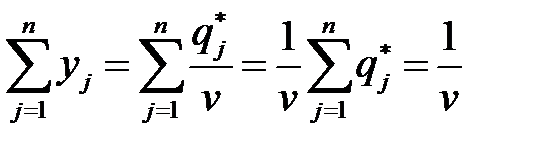 .
.
Игрок В стремится сделать свой проигрыш 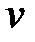 наименьшим, а, следовательно, будет возрастать величина
наименьшим, а, следовательно, будет возрастать величина
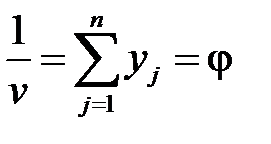 . (6.7)
. (6.7)
Учитывая выше сказанное, приходим к линейной оптимизационной модели, записанной в симметричной форме: максимизировать линейную функцию
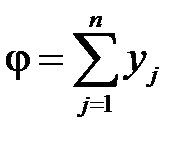
 max, (6.8)
max, (6.8)
при линейных ограничениях:
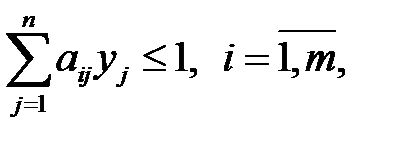 (6.9)
(6.9)
 (6.10)
(6.10)
Решив ее, найдем оптимальный план 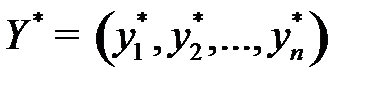 и
и  , а затем, используя (6.7) и (6.5), определим цену игры
, а затем, используя (6.7) и (6.5), определим цену игры 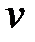 и компоненты оптимальной смешанной стратегии
и компоненты оптимальной смешанной стратегии 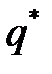 :
:
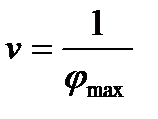 ,
, 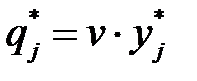 ,
,  .
.
Аналогично можно построить еще одну линейную оптимизационную модель для определения оптимальной смешенной стратегии игрока 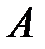 , рассмотрев неравенства
, рассмотрев неравенства
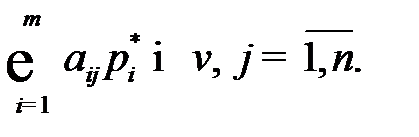
Минимизировать функцию:
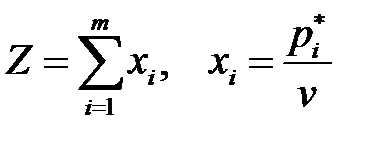 (6.11)
(6.11)
при ограничениях:
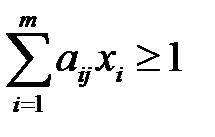 ,
, 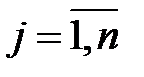 , (6.12)
, (6.12)
 ,
, 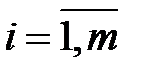 . (6.13)
. (6.13)
Решая ее, найдем оптимальный план: 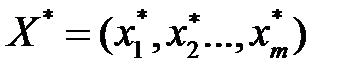 и
и 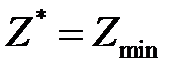 , а затем найдем цену, и оптимальную смешанную стратегию
, а затем найдем цену, и оптимальную смешанную стратегию  игрока А:
игрока А:
 ,
, 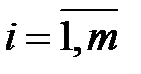 .
.
Модели (6.8)-(6.10) и (6.11)-(6.13) образуют пару двойственных линейных оптимизационных моделей.
Найдя решение одной из них, решение другой находим из строки целевой функции последней симплексной таблицы, воспользовавшись соответствием между переменными:
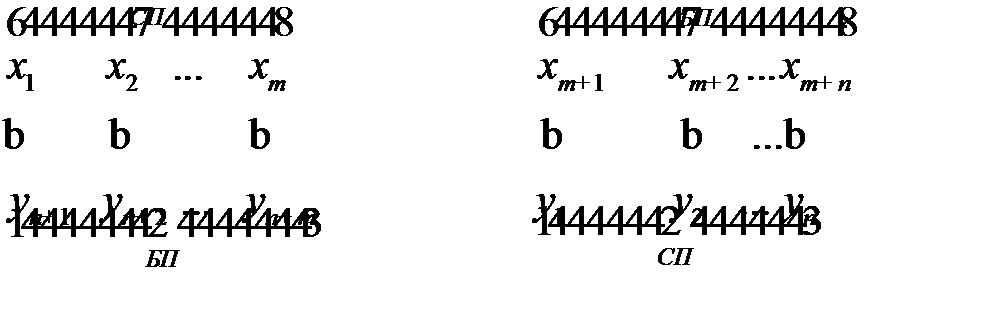
При решении матричных игр размерностью  и
и 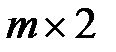 целесообразно использовать графический метод.
целесообразно использовать графический метод.
Пример 6.4. Найти решение игры с матрицей
 .
.
Решение. Найдем сначала оптимальную смешанную стратегию 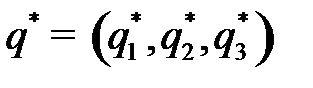 игрока В.
игрока В.
Для этого составим линейную оптимизационную модель: найти план 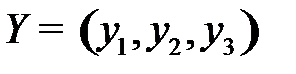 , при котором целевая функция
, при котором целевая функция
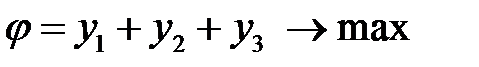 ,
,
и который удовлетворяет ограничениям:
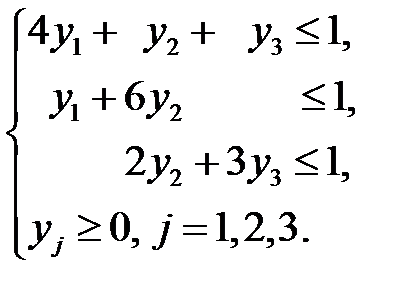
Эту модель решаем симплекс-методом. Сначала вводим неотрицательные вспомогательные переменные  и приводим систему ограничений к предпочтительному виду:
и приводим систему ограничений к предпочтительному виду:
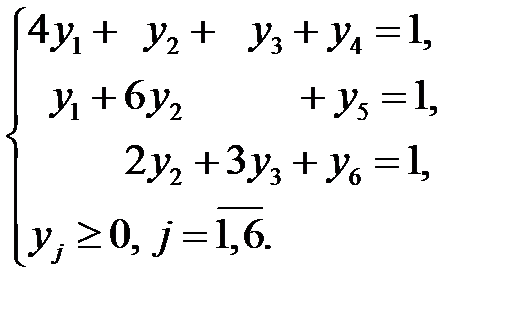
Составляем первую симплексную таблицу
| БП | 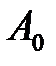
| СП | ||
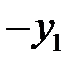
| 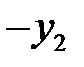
| 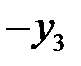
| ||
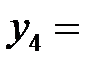
| 
| |||
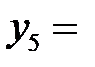
| ||||
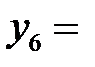
| ||||
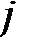
| –1 | –1 | –1 |
и находим решение в следующих симплексных таблицах:
| БП | 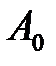
| СП | ||
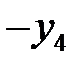
| 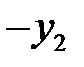
| 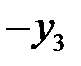
| ||

| 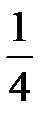
| 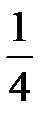
| 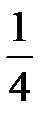
| 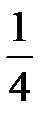
|
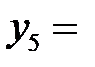
| 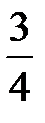
| 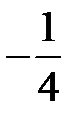
| 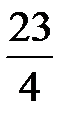
| 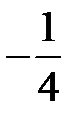
|
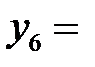
| 
| |||
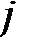
| 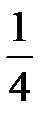
| 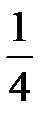
| 
| 
|
| БП | 
| СП | ||
| 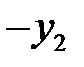
| 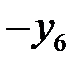
| ||

| 
| 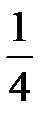
| 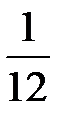
| 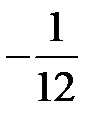
|
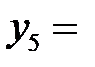
| 
| 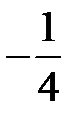
| 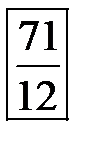
| 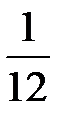
|
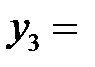
| 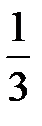
| 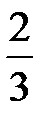
| 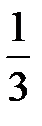
| |
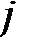
| 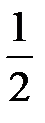
| 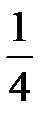
| 
| 
|
| БП | 
| СП | ||
| 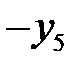
| 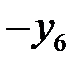
| ||

| 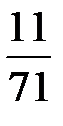
| 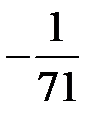
| ||
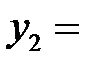
| 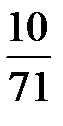
| 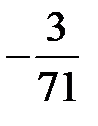
| 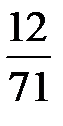
| 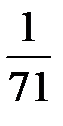
|
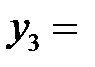
| 
| 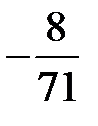
| ||
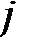
| 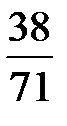
| 
| 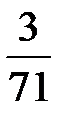
| 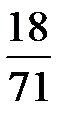
|
В последней симплексной таблице получено оптимальное решение:
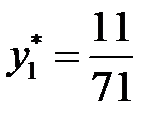 ,
, 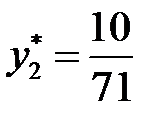 ,
, 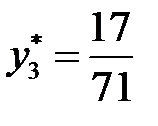 ,
,  .
.
Цену игры и компоненты оптимальной смешанной стратегии 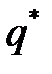 определим по формулам
определим по формулам 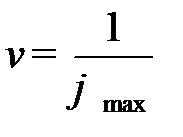 и
и 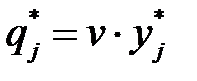 :
:
 ,
, 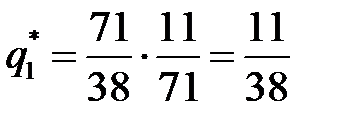 ,
,  ,
, 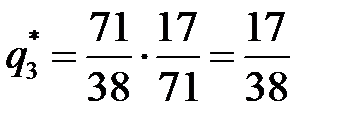 .
.
Таким образом, 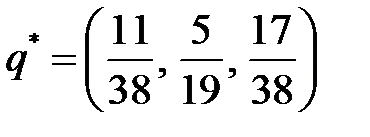 .
.
Аналогично строим модель для определения оптимальной смешанной стратегии игрока А.
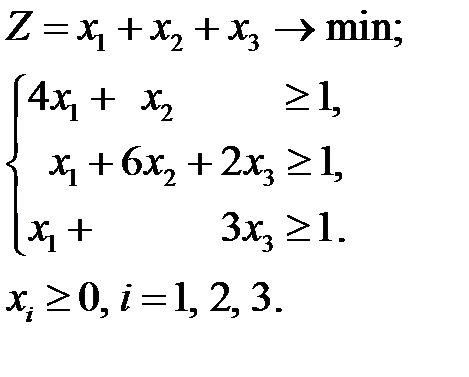
Преобразуем модель к каноническому виду, вычитая вспомогательные неотрицательные переменные 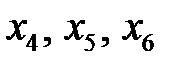 :
:
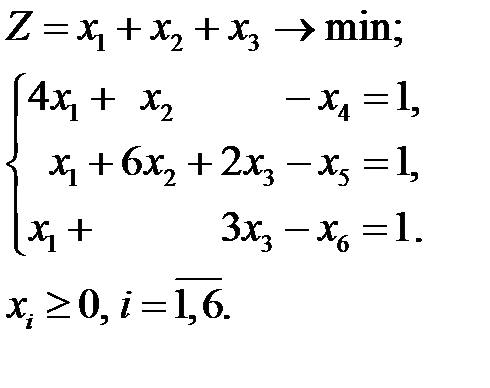
Решение этой модели находим, воспользовавшись соответствием между переменными исходной и двойственной моделей:
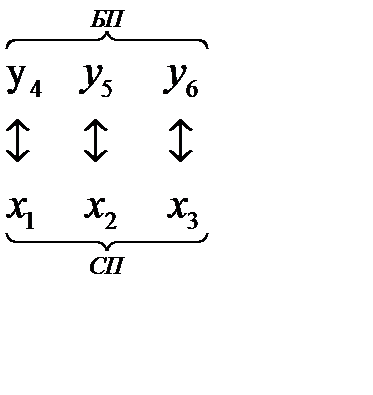

Оптимальное решение двойственной модели находим из последней симплексной таблицы, учитывая соответствие между переменными:  ,
, 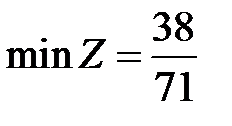 . Оптимальную смешанную стратегию игрока А определим по формулам:
. Оптимальную смешанную стратегию игрока А определим по формулам: 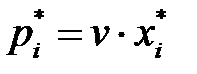 ,
, 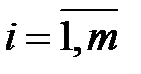 . Отсюда,
. Отсюда, 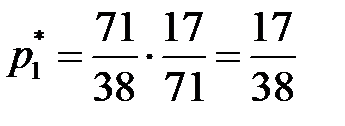 ,
,  ,
, 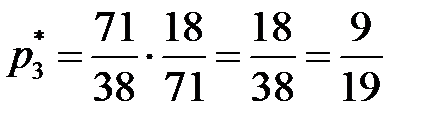 .
.
Таким образом, оптимальная смешенная стратегия игрока 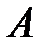 имеет вид:
имеет вид:
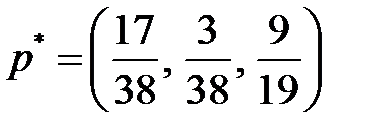 .
.
Пример 6.5.Два банка 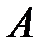 и
и  выделяют денежные средства на финансирование трех проектов. С учетом особенностей вкладов и выдачи кредитов прибыль банка
выделяют денежные средства на финансирование трех проектов. С учетом особенностей вкладов и выдачи кредитов прибыль банка  в зависимости от объемов финансирования определяется элементами матрицы
в зависимости от объемов финансирования определяется элементами матрицы
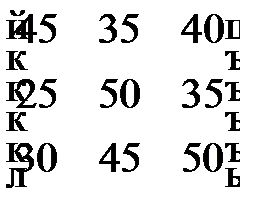 .
.
Предположим, что потери банка  при этом равны прибыли
при этом равны прибыли
банка  . Определить оптимальные смешанные стратегии банков
. Определить оптимальные смешанные стратегии банков 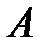 и
и 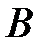 .
.
Решение. Предположим, что банк 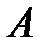 располагает суммой в
располагает суммой в 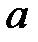 ден. ед., отпускаемой на финансирование трех проектов. Тогда чистая стратегия
ден. ед., отпускаемой на финансирование трех проектов. Тогда чистая стратегия 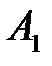 - это сумма в
- это сумма в 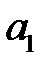 ден. ед. выделенная на финансирование первого проекта; чистая стратегия
ден. ед. выделенная на финансирование первого проекта; чистая стратегия 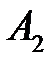 - это сумма в
- это сумма в 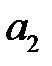 ден. ед. выделенная на финансирование второго проекта; чистая стратегия
ден. ед. выделенная на финансирование второго проекта; чистая стратегия 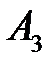 - это сумма в
- это сумма в 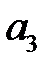 ден. ед. выделенная на финансирование третьего проекта. Банк
ден. ед. выделенная на финансирование третьего проекта. Банк 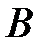 также располагает суммой в
также располагает суммой в 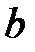 ден. ед., отпускаемой на финансирование трех проектов. Чистые стратегии
ден. ед., отпускаемой на финансирование трех проектов. Чистые стратегии 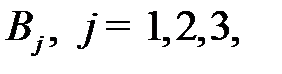 - это суммы в
- это суммы в 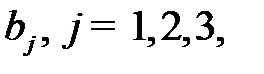 ден. ед., выделенные на финансирование трех проектов. Общие суммы средств, выделенных на финансирование трех проектов, удовлетворяют равенствам:
ден. ед., выделенные на финансирование трех проектов. Общие суммы средств, выделенных на финансирование трех проектов, удовлетворяют равенствам: 
Решим игру в чистых стратегиях. Для этого составим платежную матрицу:

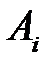
| 
| 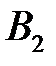
| 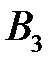
| 
|
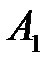
| ||||
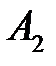
| ||||
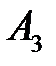
| ||||
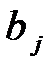
|
Из матрицы видим, что 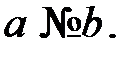 Следовательно, игра не имеет решения в чистых стратегиях. Поэтому решение игры найдем в смешенных стратегиях. Цена игры
Следовательно, игра не имеет решения в чистых стратегиях. Поэтому решение игры найдем в смешенных стратегиях. Цена игры 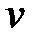 заключена между нижней
заключена между нижней 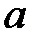 и верхней
и верхней 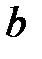 чистыми ценами, т.е.
чистыми ценами, т.е. 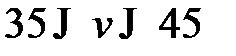 .
.
Составим математические модели для каждого игрока, предварительно упростив матрицу: разделим все элементы платежной матрицы на 5 и вычтем из полученных элементов 4. Получим матрицу  . Цена в упрощенной матичной игре будет равна:
. Цена в упрощенной матичной игре будет равна: 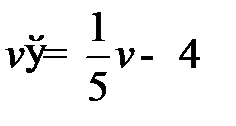 , где
, где 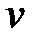 цена в исходной игре. С учетом упрощения математическая модель для игрока
цена в исходной игре. С учетом упрощения математическая модель для игрока  будет иметь вид:
будет иметь вид:
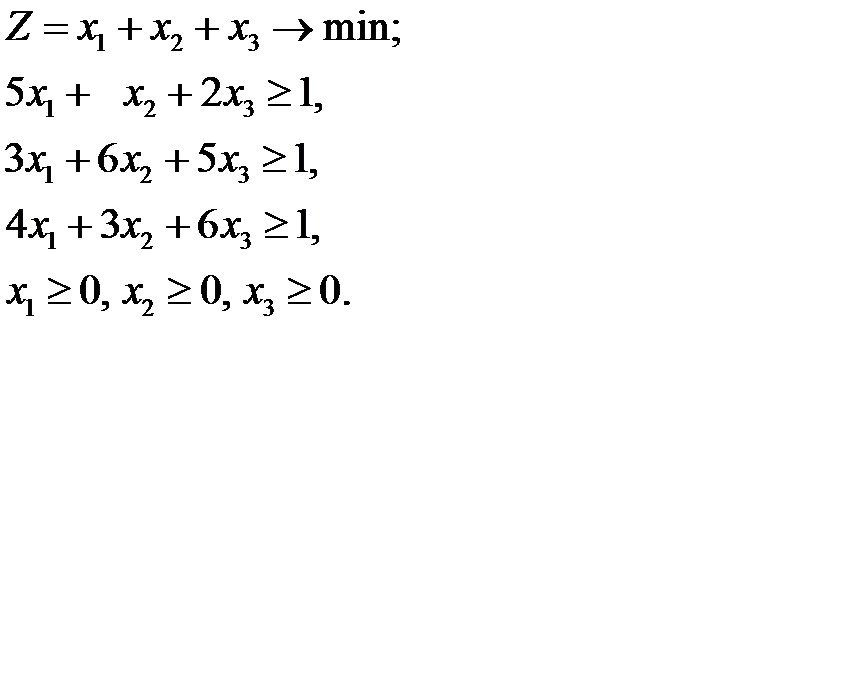
Для игрока  :
: 
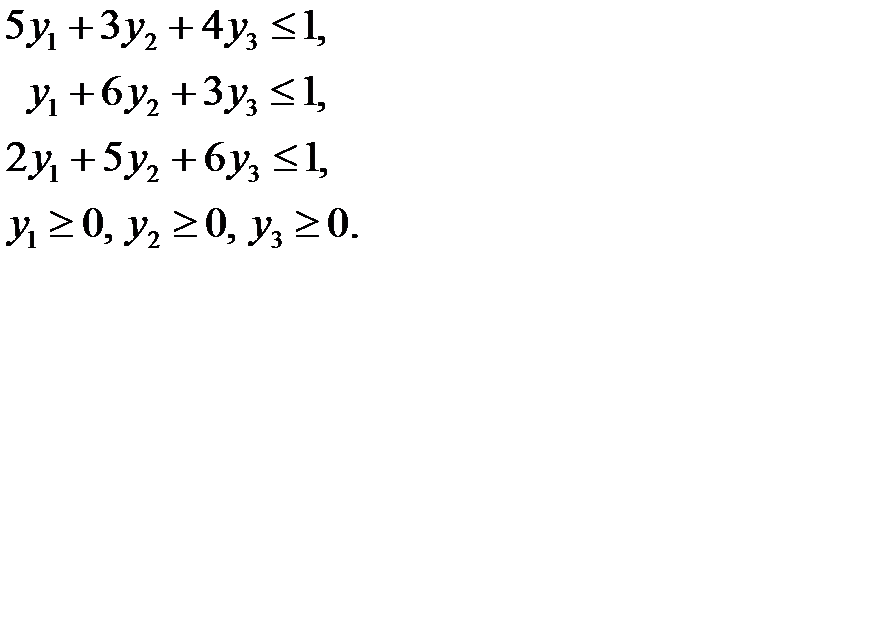
Преобразуем модели к канонической форме записи, вводя вспомогательные переменные 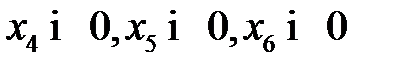 для исходной модели и
для исходной модели и 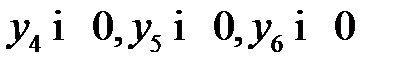 для двойственной модели. Введенные вспомогательные переменные примем за базисные переменные. Укажем соответствие между переменными пары взаимно двойственных моделей:
для двойственной модели. Введенные вспомогательные переменные примем за базисные переменные. Укажем соответствие между переменными пары взаимно двойственных моделей:
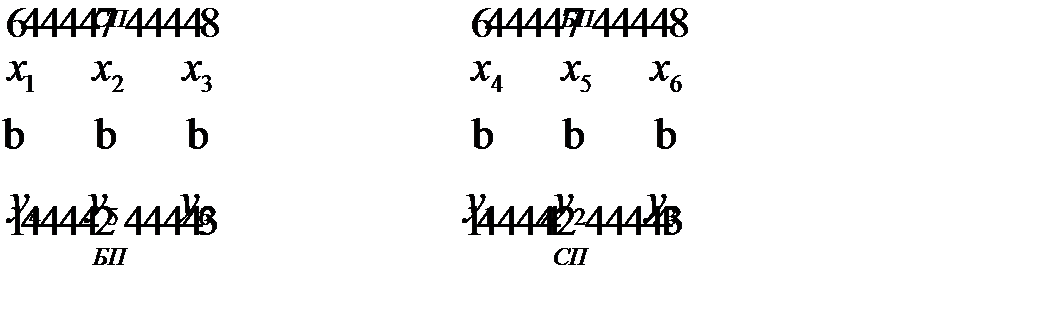
Решим двойственную модель (модель игрока 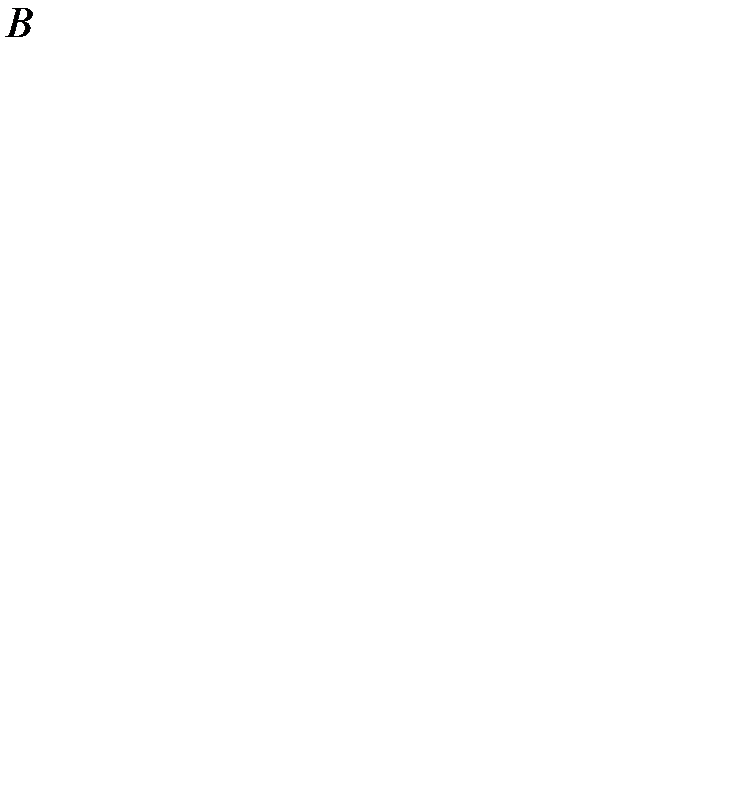 ) симплексным методом. Каноническая форма записи этой модели имеет вид:
) симплексным методом. Каноническая форма записи этой модели имеет вид:

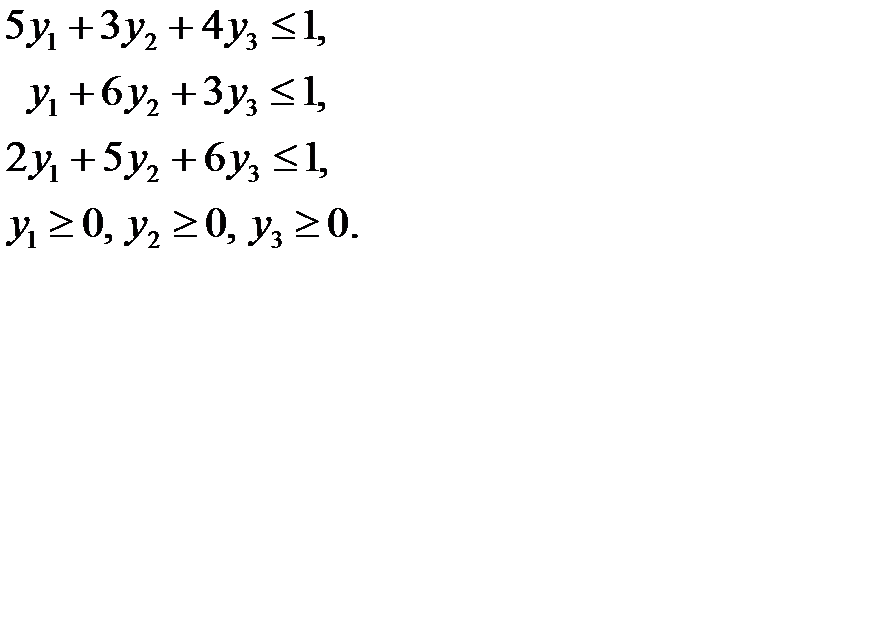
Составим симплексную таблицу:
| БП | 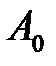
| СП | ||
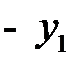
| 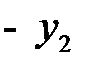
| 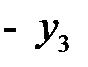
| ||
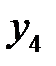
| 
| |||
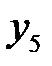
| ||||

| ||||
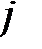
| -1 | -1 | -1 |

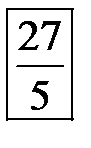
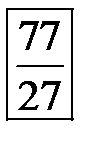
Последовательно преобразуем первоначальную симплексную таблицу:
| БП | 
| СП | ||
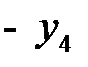
| 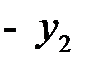
| 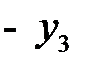
| ||

| 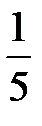
| 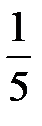
| 
| 
|
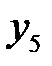
| 
| 
| 
| 
|
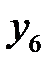
| 
| 
| 
| 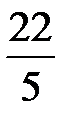
|
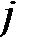
| 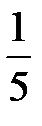
| 
| 
| 
|
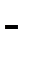
| БП | 
| СП | ||
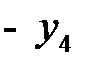
| 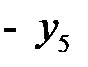
| 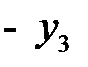
| ||
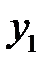
| 
| 
| 
| 
|
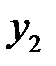
| 
| 
| 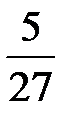
| 
|
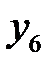
| 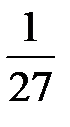
| 
| 
| 
|
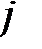
| 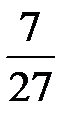
| 
| 
| 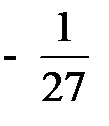
|
| БП | 
| СП | ||
| 
| 
| ||
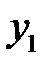
| 
| |||
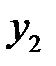
| 
| |||
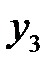
| 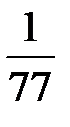
| |||
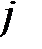
| 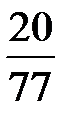
| 
| 
| 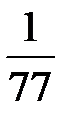
|
В последней симплексной таблице содержится оптимальный план:  ;
; 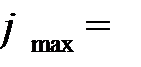
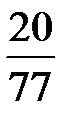 . Учитывая соответствие между переменными, находим оптимальный план игрока
. Учитывая соответствие между переменными, находим оптимальный план игрока 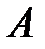 :
:  ;
; 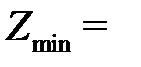
 .
.
Применяя формулы 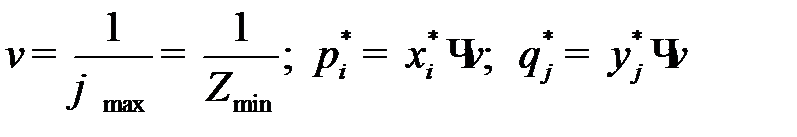 , находим цену игры и вероятности
, находим цену игры и вероятности 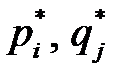 для оптимальных смешанных стратегий:
для оптимальных смешанных стратегий:  ;
; 
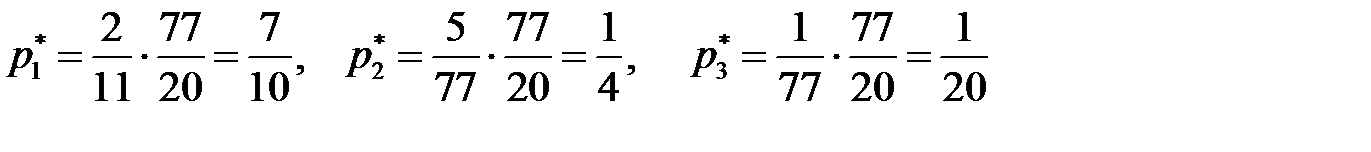 ;
;  ;
;
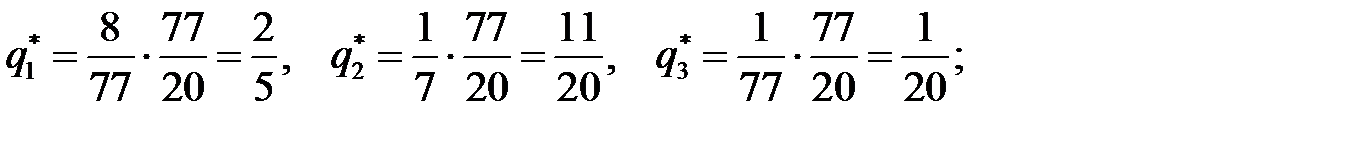
 .
.
Таким образом, применяя свою смешанную стратегию  , банк
, банк 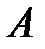 получит прибыль не менее
получит прибыль не менее 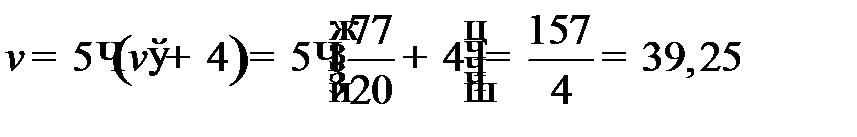 ден. ед., а убыток банка
ден. ед., а убыток банка 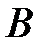 при применении своей смешанной стратегии
при применении своей смешанной стратегии  , составит не более 39,25 ден. ед.
, составит не более 39,25 ден. ед.
Следовательно, из общей суммы средств  ден. ед., выделяемых банком
ден. ед., выделяемых банком 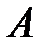 на финансирование трех проектов, на долю первого проекта должно выделяться 70%, второго – 25%, третьего – 5% этой суммы. Банк
на финансирование трех проектов, на долю первого проекта должно выделяться 70%, второго – 25%, третьего – 5% этой суммы. Банк 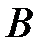 распределяет выделенные средства
распределяет выделенные средства 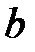 ден. ед. следующим образом: на финансирование первого проекта – 40%, второго – 55%, третьего – 5%. Такое распределение денежных средств банками
ден. ед. следующим образом: на финансирование первого проекта – 40%, второго – 55%, третьего – 5%. Такое распределение денежных средств банками 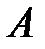 и
и 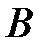 на финансирование трех проектов позволит им получить максимальную прибыль равную 39,25 ден. ед.
на финансирование трех проектов позволит им получить максимальную прибыль равную 39,25 ден. ед.
Лекция 7 Экономико-математические методы и модели финансов и кредита (продолжение)
Вопросы, изучаемые на лекции:
7.1. Статистические модели в сфере финансово-кредитной деятельности
7.2. Правила выбора оптимальной стратегии
Дата добавления: 2015-09-29; просмотров: 1457;
