Статистические модели в сфере финансово-кредитной деятельности

Изучая матричные игры, мы предполагали, что каждый из игроков (участников) стремится к наилучшему для себя результату. На практике же встречаются игры, ситуации, когда один из игроков безразличен к результату игры. Например, управление производственными процессами осуществляется путем реализации последовательности принимаемых решений. Для принятия эффективных решений необходима информация о состоянии объекта управления. С целью уменьшения неблагоприятных последствий в каждом конкретном случае следует учитывать степень риска. В приведенном примере, лицо (или группу лиц), принимающее решение, вступает в игровые отношения с некоторым абстрактным участником игры. В качестве такого игрока выступает «природа». Под природой понимается комплекс внешних обстоятельств (условий), при которых приходится принимать решение. В такой ситуации игрока (группу лиц, объединенных общностью цели) называют статистиком, а игры, в которых одним из участников является человек (игрок А), а другим природа (игрок ), называются статистическими. Ясно, что природа развивается по объективным законам, независимо от человека, который не всегда знает или знает не полно эти законы. Поэтому, принимая решения, человек должен учитывать их последствия. Любую хозяйственную деятельность человека можно рассматривать как игру с природой.

Как и в матричных играх, игрок А может использовать стратегии 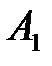, , 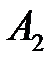…, 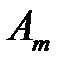. Множество состояний природы назовем множеством стратегий , имея в виду полную совокупность внешних условий, в которых статистику А приходится выбирать свою стратегию. Статистику А обычно известны возможные состояния природы 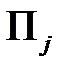, а иногда вероятности 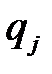с которыми она реализует эти состояния. Эти вероятности называются априорными. Проводя эксперименты, статистик может уточнить состояния 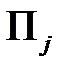и их вероятности 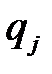, которые называются апостериорными.

Мы рассмотрим статистические игры без эксперимента.

Статистик в своих взаимоотношениях с природой может пользоваться как чистыми стратегиями 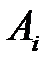, так и смешанными:

, ,

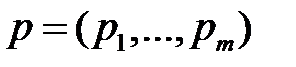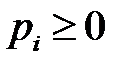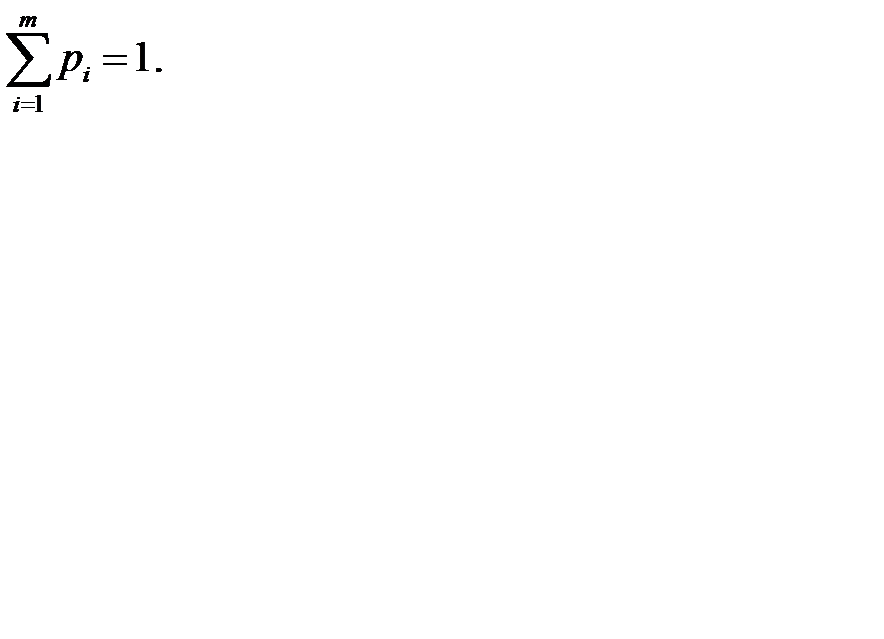
Если статистику А известны числа 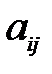, характеризующие пару стратегий ( 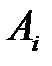, 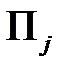), то статистическую игру можно задать платежной матрицей .

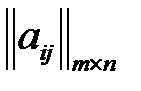Пример 6.6. В фирме «Плюс» при производстве продукции потребляется 20-22 единицы сырья S, в зависимости от его качества. Если для выпуска запланированной продукции сырья окажется недостаточно, то запас его можно пополнить, но одна единица сырья при этом будет стоить 10 ден. ед. Если же запас сырья будет большим, то на хранение и содержание единицы сырья нужно затратить 7 ден.ед.

Придадим описанной ситуации игровую схему. В качестве статистика (игрок А) выступает администрация предприятия, которая может заказать 20, 21 или 22 единицы сырья (стратегии 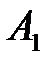, , 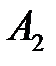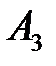). Вторым игроком (природа ) может выступать фактический расход сырья в процессе производства. Расход сырья зависит от качества сырья и составляет 20, 21 или 22 единицы сырья (состояния природы , , 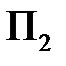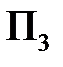). Элементы матрицы 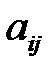характеризуют дополнительные затраты, вызванные доставкой сырья в случае недостатка или хранением в случае избытка.

Паре стратегий ( 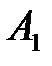, 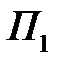) соответствует число 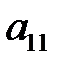= 0, так как расход и закупка сырья равны.

Паре стратегий ( 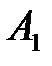, 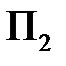) соответствует число 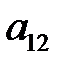= –10, так как расход превысит запасы и нужно закупить одну единицу сырья.

Паре стратегий ( 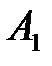, 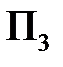) соответствует число 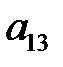= –20, закупить нужно 2 единицы сырья.

Паре стратегий ( 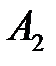, ) соответствует число 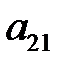= –7, так как придется хранить 1 единицу сырья, что вызовет затраты 7 ден. ед. и т.д.

Таким образом, рассматриваемую ситуацию можно описать при помощи платежной матрицы:

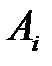
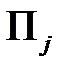
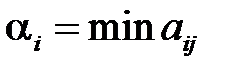
П (20)	П (21)	П (22)
А (20)		–10	–20	–20
А (21)	–7		–10	–10
А (22)	–14	–7		–14
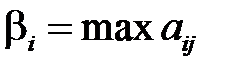
				-10

Данная игра не имеет решения в чистых стратегиях, так как .