Математическая модель транспортной задачи. Общая постановка транспортной задачи
Общая постановка транспортной задачи. Пусть имеется m ( 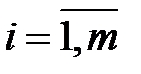 ) поставщиков, располагающих некоторой однородной продукцией в объемах
) поставщиков, располагающих некоторой однородной продукцией в объемах 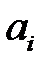 ,
, 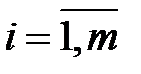 , единиц соответственно, которая должна быть доставлена n (j =
, единиц соответственно, которая должна быть доставлена n (j = 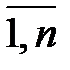 ) потребителям с объемами потребления по
) потребителям с объемами потребления по 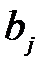 единиц. Задана матрица
единиц. Задана матрица 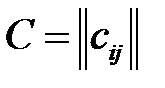 , где
, где 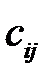 – стоимость перевозки единицы продукции от i-го поставщика j-му потребителю, называемой матрицей тарифов (издержек или транспортных расходов). Требуется составить план перевозок
– стоимость перевозки единицы продукции от i-го поставщика j-му потребителю, называемой матрицей тарифов (издержек или транспортных расходов). Требуется составить план перевозок 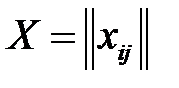 , т. е. найти, сколько единиц продукции должно быть отправлено из i-го пункта отправления в j-й пункт потребления так, чтобы суммарные издержки на перевозки были минимальными. При этом продукция от производителей должна быть полностью вывезена, а потребности потребителей должны быть удовлетворены.
, т. е. найти, сколько единиц продукции должно быть отправлено из i-го пункта отправления в j-й пункт потребления так, чтобы суммарные издержки на перевозки были минимальными. При этом продукция от производителей должна быть полностью вывезена, а потребности потребителей должны быть удовлетворены.
Для наглядности условия транспортной задачи можно представить в виде распределительной таблицы (таблица 5.1).
Таблица 5.1
Поставщики
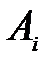
| Потребители 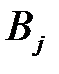
| Запас однородного продукта | ||||
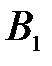
| … | 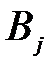
| … | 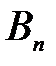
| ||
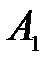
| 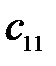
| … | с 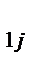
| … | 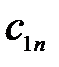
| 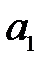
|
| … | … | … | … | … | … | … |
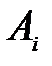
| 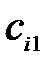
| … | 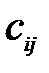
| … | 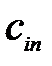
| 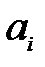
|
| … | … | … | … | … | … | … |
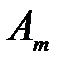
| 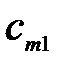
| … | 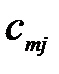
| … | 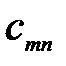
| 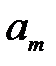
|
| Потребность в продукте | 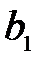
| … | 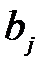
| … | 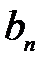
|
Если 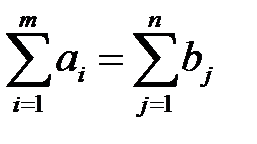 , то задача называется закрытой, в противном случае – т.е. если
, то задача называется закрытой, в противном случае – т.е. если 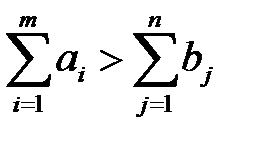 или
или 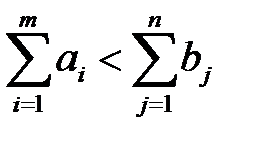 - открытой.
- открытой.
Построим математическую модель закрытой задачи. Для этого обозначим через 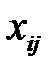 – количество груза, перевозимого от i-го поставщика j-му потребителю. Требуется построить планперевозок продукции, матрицу
– количество груза, перевозимого от i-го поставщика j-му потребителю. Требуется построить планперевозок продукции, матрицу 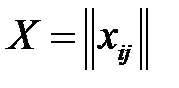 ,
, 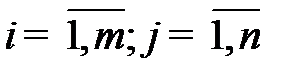 . При этом целевая функция, описывающая общие суммарные затраты, связанные с реализацией плана перевозок, должна стремиться к минимуму:
. При этом целевая функция, описывающая общие суммарные затраты, связанные с реализацией плана перевозок, должна стремиться к минимуму:
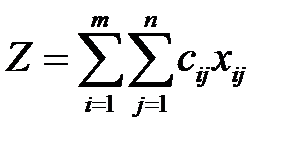
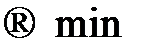 (5.1)
(5.1)
Запишем ограничения, которым должны удовлетворять переменные величины 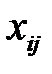 , учитывая, что:
, учитывая, что:
а) запасы продукции у поставщиков должны быть полностью вывезены:
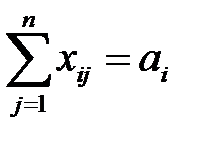 ,
, 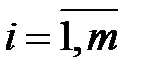 ; (5.2)
; (5.2)
б) запросы потребителей должны быть полностью удовлетворены:
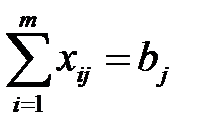 ,
, 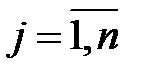 ; (5.3)
; (5.3)
в) должны быть устранены обратные перевозки – условие неотрицательности:
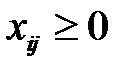 ,
, 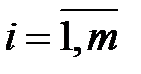 ,
, 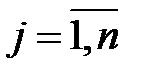 . (5.4)
. (5.4)
Матрицу 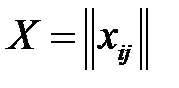 , удовлетворяющую ограничениям (5.2)-(5.4), называют допустимым планом перевозок, а переменные
, удовлетворяющую ограничениям (5.2)-(5.4), называют допустимым планом перевозок, а переменные 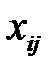 – допустимыми перевозками.
– допустимыми перевозками.
Таким образом, транспортная задача формулируется так: требуется найти среди допустимых планов перевозок такой план, который доставляет целевой функции (5.1) минимальное значение.
Допустимый план Х, доставляющий целевой функции (5.1) минимальное значение, называется оптимальным.
Транспортную задачу можно сформулировать и в сетевой форме.
Отрезок или линию, соединяющую i-го поставщика с j-м потребителем, назовем коммуникацией и обозначим (ij) или ( 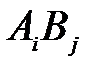 ). Если на всех коммуникациях (ij) поставлены величины перевозок
). Если на всех коммуникациях (ij) поставлены величины перевозок 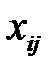 , то получим транспортную сеть. Графический способ задания транспортной задачи указан на рис. 5.1.
, то получим транспортную сеть. Графический способ задания транспортной задачи указан на рис. 5.1.
| Поставщики |
| A1 |
| Ai |
| … |
| Am |
| Потребители |
| B1 |
| Bj |
| Bn |
| … |
| x11 |
| x1j |
| x1n |
| xi1 |
| xij |
| xin |
| xm1 |
| xmj |
| xmn |
| … |
| … |
| Рисунок 5.1. |
Дата добавления: 2015-09-29; просмотров: 796;
