Теоремы двойственности
Рассмотрим пару взаимно двойственных моделей:
Прямая. Требуется максимизировать функцию
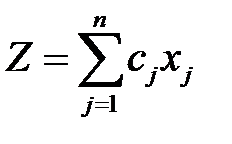 → max , (3.14)
→ max , (3.14)
при ограничениях
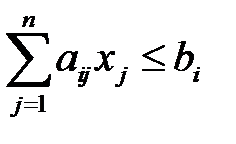 ,
, 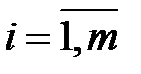 , (3.15)
, (3.15)
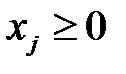 , j =
, j = 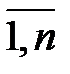
Двойственная. Требуется минимизировать функцию
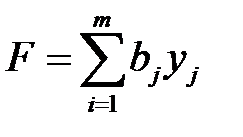 → min, (3.16)
→ min, (3.16)
при ограничениях
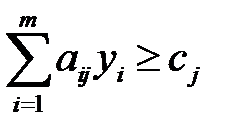 , j =
, j = 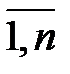 , (3.17)
, (3.17)
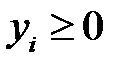 ,
, 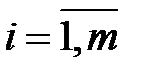 .
.
Относительно допустимых планов двойственных моделей сформулируем следующие утверждения.
Теорема 3.1. Для любых допустимых планов
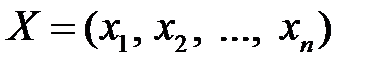 и
и 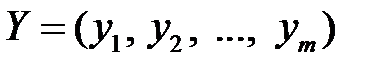
прямой и двойственной моделей всегда справедливо неравенство:
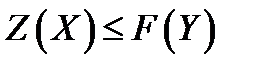 или
или 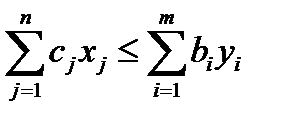 . (3.18)
. (3.18)
Это неравенство называется основным неравенством теории двойственности.
Действительно, умножив неравенство (3.15) на 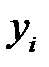 и просуммировав по индексу
и просуммировав по индексу 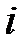 , неравенство можно переписать в виде:
, неравенство можно переписать в виде:
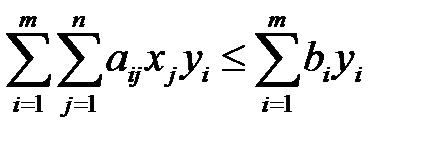 . (3.19)
. (3.19)
Умножая неравенство (3.17) на 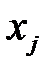 и суммируя по индексу
и суммируя по индексу  , получим:
, получим:
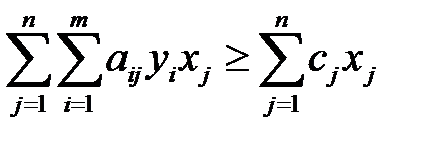 . (3.20)
. (3.20)
Поскольку в неравенствах (3.19) и (3.20) левые части равны, то, сравнивая их, получаем основное неравенство теории двойственности (3.18).
С экономической точки зрения, неравенство (3.18) означает, что для любого допустимого плана производства и любого допустимого вектора оценок ресурсов стоимость изготовленного продукта не превосходит оценки ресурсов.
Теорема 3.2. (Достаточный признак оптимальности).Если для некоторых допустимых планов 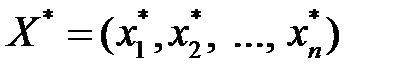 и
и 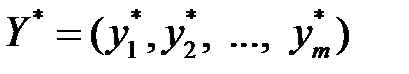 пары двойственных моделей выполняется равенство
пары двойственных моделей выполняется равенство 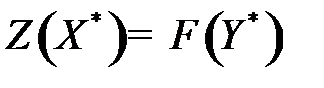 , то
, то 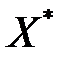 – оптимальный план (3.14) – (3.15), а
– оптимальный план (3.14) – (3.15), а 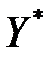 – оптимальный план модели (3.16) – (3.17).
– оптимальный план модели (3.16) – (3.17).
Действительно, пусть 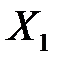 – любой допустимый план задачи (3.14) – (3.15), тогда в силу неравенства (3.18) выполняется неравенство:
– любой допустимый план задачи (3.14) – (3.15), тогда в силу неравенства (3.18) выполняется неравенство: 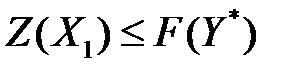 . Но так как по условию
. Но так как по условию 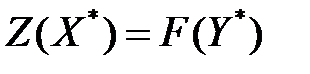 , то
, то 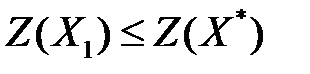 . В силу произвольности допустимого плана
. В силу произвольности допустимого плана 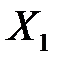 следует, что
следует, что 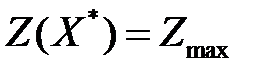 , т. е.
, т. е. 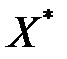 – оптимальный план задачи (3.14) – (3.15).
– оптимальный план задачи (3.14) – (3.15).
Пусть теперь 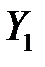 – любой допустимый план двойственности задачи (3.16)- – (3.17). Из неравенства (3.18) следует, что
– любой допустимый план двойственности задачи (3.16)- – (3.17). Из неравенства (3.18) следует, что 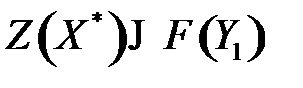 . Но так как
. Но так как 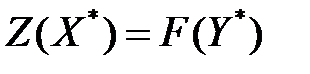 , то
, то 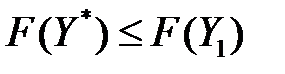 , а поскольку
, а поскольку 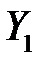 произвольный план, то
произвольный план, то 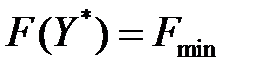 , следовательно
, следовательно 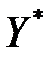 – оптимальный план модели (3.16) - (3.17).
– оптимальный план модели (3.16) - (3.17).
Теорема 3.3 (теорема существования оптимальных планов).Для того чтобы прямая и двойственная модели имели оптимальный план, необходимо и достаточно, чтобы для каждой из них существовал хотя один допустимый план.
Доказательство. Необходимость. Пусть пара двойственных моделей имеет оптимальные планы 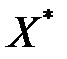 и
и 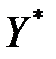 :
: 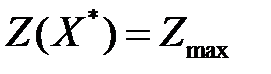 ,
, 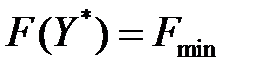 ,
, 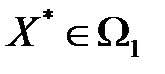 ,
, 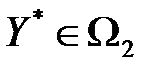 ,
, 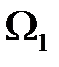 и
и 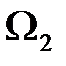 – множества допустимых решений моделей. Это означает, что множества не пустые, так как имеют хотя бы по одному допустимому плану.
– множества допустимых решений моделей. Это означает, что множества не пустые, так как имеют хотя бы по одному допустимому плану.
Достаточность. Пусть 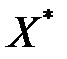 и
и 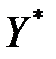 – допустимые планы пары двойственных моделей. Рассмотрим допустимый план
– допустимые планы пары двойственных моделей. Рассмотрим допустимый план 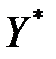 модели (3.16) - (3.17) и произвольный допустимый план Х модели (3.14) - (3.15), тогда в силу основного неравенства теории двойственности можно записать неравенство:
модели (3.16) - (3.17) и произвольный допустимый план Х модели (3.14) - (3.15), тогда в силу основного неравенства теории двойственности можно записать неравенство:
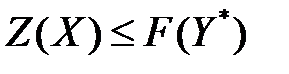 .
.
Решая задачу (3.14)-(3.15) симплекс-методом от допустимого плана Х перейдем к опорным планам 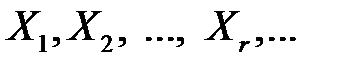 , для которых выполняются неравенства
, для которых выполняются неравенства 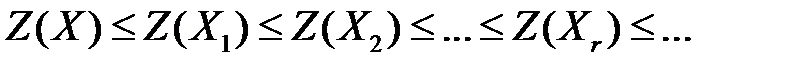 . Значит, последовательность
. Значит, последовательность 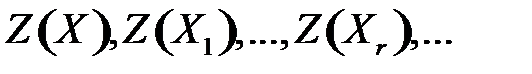 значений целевой функции неубывающая и ограничена сверху, поскольку все
значений целевой функции неубывающая и ограничена сверху, поскольку все 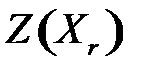 не превосходят
не превосходят 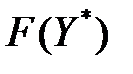 . Такая последовательность сходится, т. е. существует такой план
. Такая последовательность сходится, т. е. существует такой план 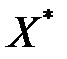 , что для всех
, что для всех 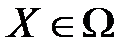 ,
, 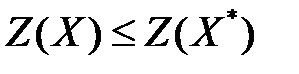 , т. е.
, т. е. 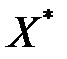 – оптимальный.
– оптимальный.
Аналогично доказывается, что 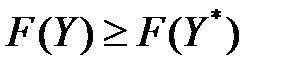 . Достаточность доказана, следовательно, доказана теорема.
. Достаточность доказана, следовательно, доказана теорема.
Теорема 3.4 (первая основная теорема двойственности). Если одна из двойственных моделей имеет оптимальный план, то и другая также имеет оптимальный план. Причем для любых оптимальных планов 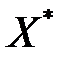 и
и 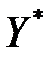 выполняется равенство:
выполняется равенство: 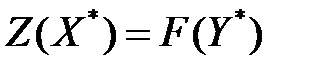 . Если же целевая функция одной из моделей не ограничена, то система ограничений другой противоречива.
. Если же целевая функция одной из моделей не ограничена, то система ограничений другой противоречива.
Рассмотрим пару симметричных двойственных моделей (3.14)-(3.15) и (3.16)-(3.17).Вводя дополнительные переменные 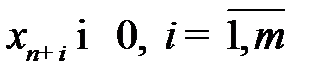 , в прямую модель и
, в прямую модель и 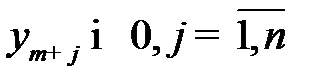 , в двойственную и учитывая, что
, в двойственную и учитывая, что 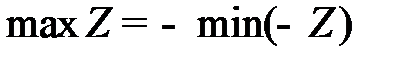 , приводим модели к канонической форме записи. Если исходная модель (3.14) - (3.15) имеет оптимальный план:
, приводим модели к канонической форме записи. Если исходная модель (3.14) - (3.15) имеет оптимальный план:
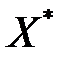 = (
= ( 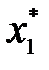 ,
, 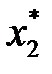 , …,
, …, 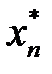 ,
, 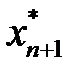 , …,
, …, 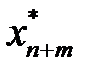 ) = (0, …, 0,
) = (0, …, 0, 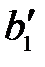 , …,
, …, 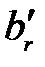 , …,
, …, 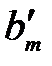 ),
),
то через конечное число шагов придем к окончательной симплексной таблице, в которой в строке целевой функции нет ни одного положительного элемента, а в столбце свободных членов – ни одного отрицательного, кроме быть может, значения целевой функции (таблица 3.15).
Этой таблице отвечает определенная симплексная таблица двойственной модели, в которой столбец свободных членов не будет содержать ни одного отрицательного элемента, а в строке целевой функции – ни одного положительного.
Это означает, что для двойственной модели также получен оптимальный план:
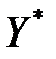 = (
= ( 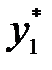 , …,
, …, 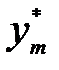 ,
, 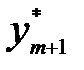 , …,
, …, 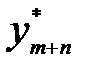 ) = (0, …, 0,
) = (0, …, 0, 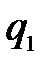 , …,
, …, 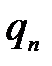 ).
).
Таблица 3.15
| БП | 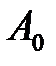
| СП |
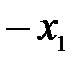 … … 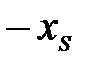 … … 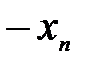
| ||

| 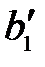
| 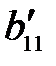 … … 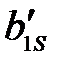 … … 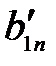
|
| … | … | . . . |
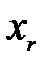
| 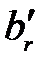
| 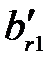 … … 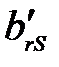 … … 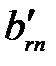
|
| … | … | . . . |
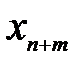
| 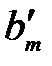
| 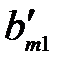 … … 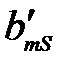 … … 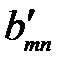
|
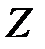
| Q | 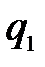 … … 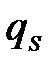 … … 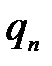
|
Значение целевой функции для данного плана:
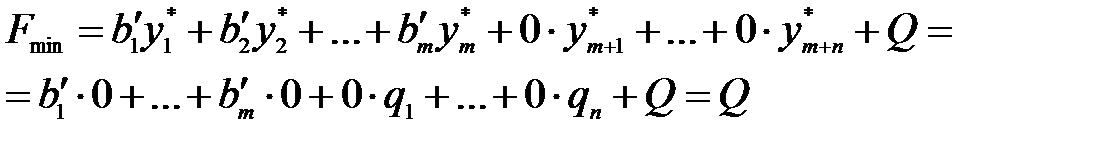
Так как в исходной задаче все свободные элементы 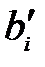 ,
, 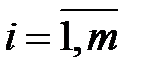 , неотрицательны, то в точке
, неотрицательны, то в точке 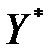 = (
= ( 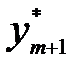 , …,
, …, 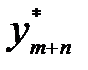 ) = (0, …, 0) целевая функция достигает min:
) = (0, …, 0) целевая функция достигает min: 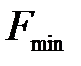 = Q. Итак, для пары двойственных задач имеет:
= Q. Итак, для пары двойственных задач имеет: 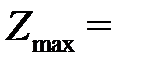
= 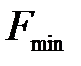 , т. е.
, т. е. 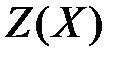 =
= 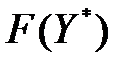 .
.
Рассмотрим случай, когда среди компонентов 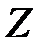 -строки имеется отрицательное число (
-строки имеется отрицательное число ( 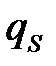 ), а в соответствующем столбце нет положительных элементов (
), а в соответствующем столбце нет положительных элементов ( 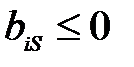 ), т. е. нельзя выбрать разрешающий элемент.
), т. е. нельзя выбрать разрешающий элемент.
Тогда свободной переменной 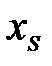 исходной задачи соответствует базисная переменная
исходной задачи соответствует базисная переменная 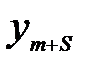 двойственной задачи, которая может быть выражена равенством:
двойственной задачи, которая может быть выражена равенством:
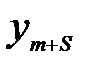 =
= 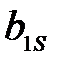
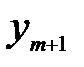 + … +
+ … + 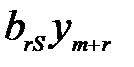 + … +
+ … + 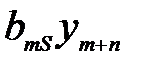 +
+ 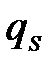 .
.
Так как 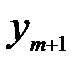 ≥ 0, …,
≥ 0, …, 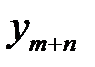 ≥ 0, а
≥ 0, а 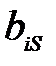 ≤ 0,
≤ 0, 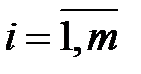 , то
, то 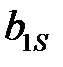
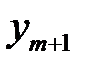 + … +
+ … + 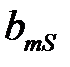
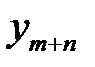 ≤ 0, т. е.
≤ 0, т. е. 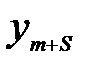 < 0. Это означает, что двойственная задача не имеет ни одного допустимого плана.
< 0. Это означает, что двойственная задача не имеет ни одного допустимого плана.
Отметим, что обратное утверждение несправедливо, т. е. если одна из двойственных задач не имеет ни одного допустимого плана, то целевая функция второй задачи не ограничена.
Экономическая интерпретация этой теоремы состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Следовательно, план производства и вектор оценок ресурсов являются оптимальными, если цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов.
Теорема 3.5 (вторая теорема двойственности о дополняющей нежесткости). Чтобы допустимые планы  и
и 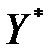 пары двойственных моделей были оптимальными, необходимо и достаточно выполнение соотношений:
пары двойственных моделей были оптимальными, необходимо и достаточно выполнение соотношений:
если 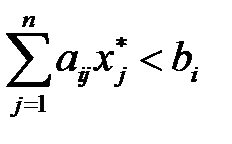 , то
, то 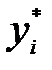 = 0,
= 0, 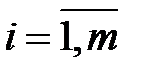 ;
;
если 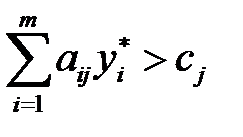 , то
, то 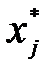 = 0,
= 0, 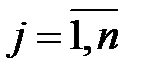 ,
,
где  ,
, 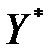 – оптимальные планы соответственно прямой и двойственной моделей.
– оптимальные планы соответственно прямой и двойственной моделей.
Доказательство. Необходимость. Пусть  и
и 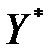 – оптимальные планы двойственных моделей (3.14)-(3.15) и (3.16)-(3.17). Для оптимальных планов имеем:
– оптимальные планы двойственных моделей (3.14)-(3.15) и (3.16)-(3.17). Для оптимальных планов имеем:
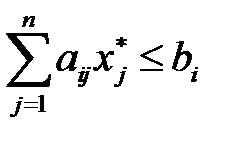 ,
, 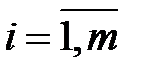 ; (3.21)
; (3.21)
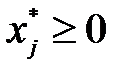 , j =
, j = 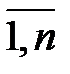 , (3.22)
, (3.22)
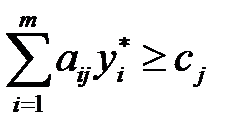 , j =
, j = 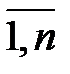 , (3.23)
, (3.23)
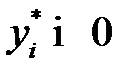 ,
, 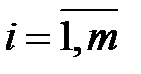 ; (3.24)
; (3.24)
Умножив неравенство (3.21) на 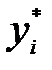 , и просуммировав по индексу i, получим:
, и просуммировав по индексу i, получим:
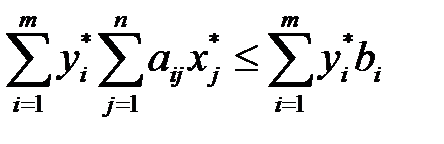 или
или 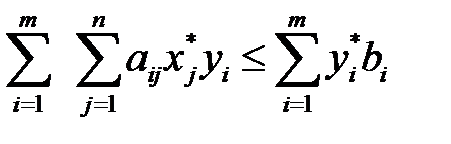 .
.
Умножив (3.23) на 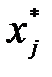 , и просуммировав по индексу
, и просуммировав по индексу  , получим:
, получим:
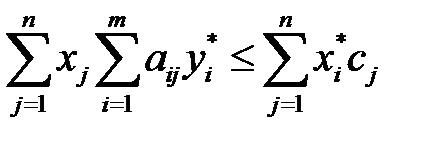 или
или 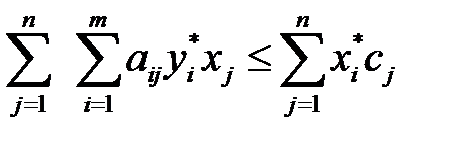 .
.
В силу теоремы 3.2 для оптимальных планов имеем равенство:
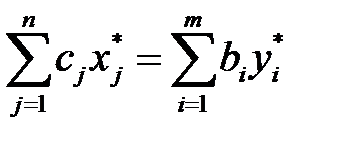
Из выше приведенных отношений имеем:
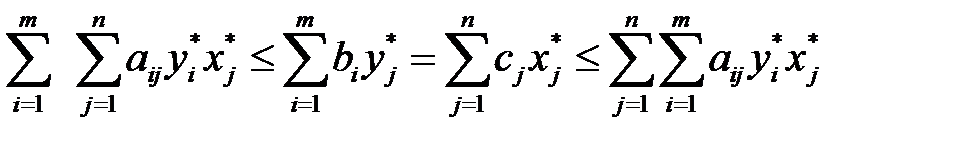
Так как крайние суммы равны:
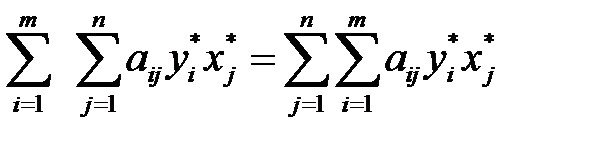 ,
,
то
 и
и 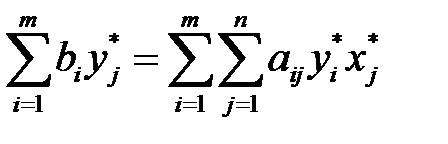 .
.
Полученные соотношения можно переписать в виде:
И .
Так как все слагаемые в суммах положительны, то:
И .
Два сомножителя равны нулю, если равен нулю хотя бы один из сомножителей. Поэтому, если например: 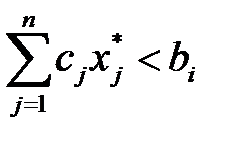 , то
, то 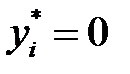 ,
,
если же 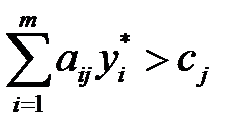 , то
, то 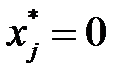 , что и требовалось доказать.
, что и требовалось доказать.
Достаточность. Пусть для некоторых планов 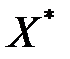 и
и 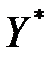 пары двойственных задач выполняются соотношения:
пары двойственных задач выполняются соотношения:
если 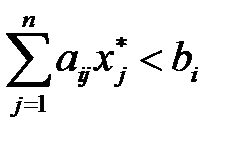 , то
, то 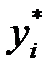 = 0,
= 0, 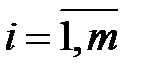 ;
;
или
если 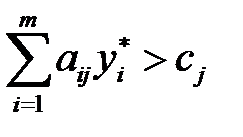 , то
, то 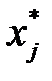 = 0, j =
= 0, j = 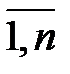 ,
,
Умножим неравенство (3.21) на 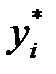 , и суммируя по i, получим:
, и суммируя по i, получим:
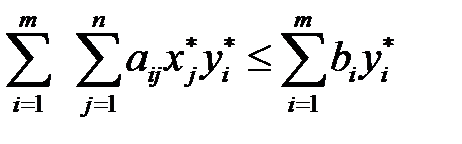 .
.
Умножая неравенство (3.23) на 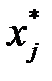 , и суммируя по
, и суммируя по  , получаем:
, получаем:
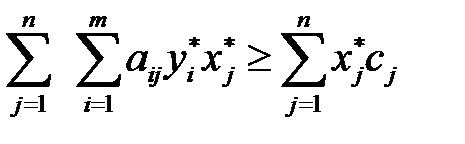 .
.
Левые части в неравенствах равны, следовательно, равны и правые части:
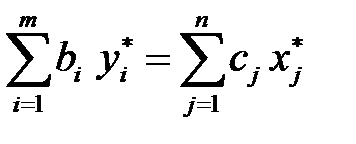 ,
,
Согласно достаточного признака оптимальности, планы 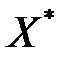 и
и 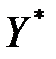 являются оптимальными для прямой и двойственной моделей. Теорема доказана.
являются оптимальными для прямой и двойственной моделей. Теорема доказана.
Вторая теорема двойственности с экономической точки зрения оценки оптимального плана – это мера дефицитности ресурсов. Ресурс, используемый в оптимальном плане производства полностью, является дефицитным, его оценка положительна. Дальнейшее его увеличение целесообразно. Если ресурс используется не полностью, то он избыточен, его дальнейшее увеличение не повлияет на эффективность предприятия. Двойственная оценка недефицитного ресурса равна нулю.
Лекция 4 Экономико-математические методы и модели оптимального планирования в промышленности, АПК (продолжение)
Вопросы, изучаемые на лекции:
4.1. Целочисленные оптимизационные модели в промышленности, АПК. Примеры. Методы решения
4.2. Алгоритм метода Гомори решения целочисленных оптимизационных моделей
Дата добавления: 2015-09-29; просмотров: 1616;
