Свойства решений линейной оптимизационной модели
Рассмотрим линейнуюоптимизационную модель с системой ограничений, записанной в каноническом виде:
 , (1.15)
, (1.15)
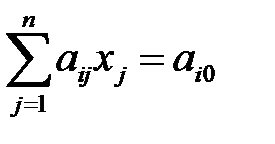 , i =
, i = 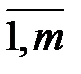 ; (1.16)
; (1.16)
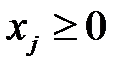 , j =
, j = 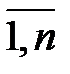 . (1.17)
. (1.17)
Система ограничений содержит m уравнений, тогда если:
1) ранг системы r = m=n, т. е. все уравнения линейно независимы и их число равно числу неизвестных, то система имеет единственное решение, и вопрос о выборе оптимального плана отпадает;
2) ранг системы меньше числа неизвестных, т.е.  , тогда система имеет бесконечное множество решений и, следовательно, возможен выбор оптимального плана.
, тогда система имеет бесконечное множество решений и, следовательно, возможен выбор оптимального плана.
Поэтому предположим, что 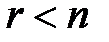 . В этом случае система векторов-столбцов
. В этом случае система векторов-столбцов 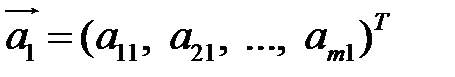 , …,
, …, 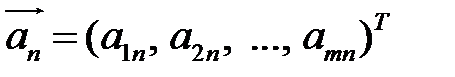 может содержать несколько базисов. Их число не превосходит
может содержать несколько базисов. Их число не превосходит 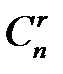 . Неизвестные, соответствующие r векторам базиса, называют базисными, а остальные n – r называют свободными неизвестными.
. Неизвестные, соответствующие r векторам базиса, называют базисными, а остальные n – r называют свободными неизвестными.
Если, например, один из базисов составляют первые r векторов  , то базисными будут неизвестные
, то базисными будут неизвестные 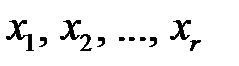 , а свободными -
, а свободными - 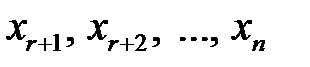 . Тогда систему ограничений (1.16) можно преобразовать к виду:
. Тогда систему ограничений (1.16) можно преобразовать к виду:
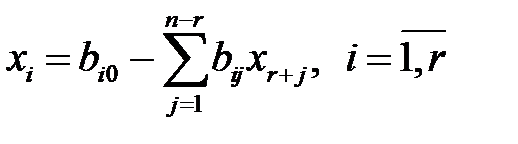 . (1.18)
. (1.18)
Запись (1.18) называют разрешенной формой системы или общим решением.
Базисное решение – частное решение, полученное из общего при нулевых значениях свободных неизвестных:
 .
.
Так как число базисов равно 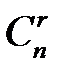 , то и базисных решений системы (1.16) будет не более
, то и базисных решений системы (1.16) будет не более 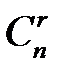 . Если в базисном решении все базисные переменные принимают неотрицательные значения, то его называют опорным. Следовательно, опорных планов не более чем
. Если в базисном решении все базисные переменные принимают неотрицательные значения, то его называют опорным. Следовательно, опорных планов не более чем 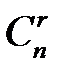 .
.
План 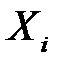 =(
=( 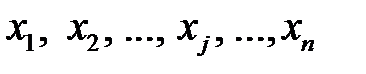 ) задачи (1.15), (1.16) называется опорным, если ненулевым положительным значениям переменных
) задачи (1.15), (1.16) называется опорным, если ненулевым положительным значениям переменных 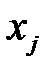 соответствуют базисные векторы
соответствуют базисные векторы 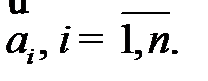
Опорный план не может содержать более чем r положительных компонент. Опорный план, содержащий ровно r отличных от нуля компонент называется невырожденным. Если же хотя бы одна из базисных компонент равна 0, то опорный план называется вырожденным.
Так как планы линейнойоптимизационной модели с геометрической точки зрения – это точки многогранника планов Ω, то опорные планы являются его вершинами.
Итак, каждому опорному плану модели (1.15), (1.16) соответствует вершина многогранника планов и, наоборот, каждой вершине многогранника планов соответствует опорный план модели (1.15), (1.16).
Более того, любой план линейнойоптимизационной модели можно представить как выпуклую линейную комбинацию ее опорных планов. Поэтому для исследования планов линейнойоптимизационной модели достаточно изучить лишь опорные планы.
Опорные планы линейнойоптимизационной модели удовлетворяют теореме.
Теорема 1.2.Если целевая функция линейнойоптимизационной модели достигает экстремального значения в некоторой точке области допустимых решений Ω, то она принимает это значение в угловой (крайней) точке, если же более чем в одной угловой (крайней) точке, то она принимает это же значение в любой их выпуклой линейной комбинации.
Доказательство. Рассмотрим линейнуюоптимизационную модель в канонической форме (1.15) – (1.17). Система ограничений (1.16) определяет многогранник Ω. Следовательно, функция  определена на замкнутом ограниченном множестве, и она достигает наибольшего значения
определена на замкнутом ограниченном множестве, и она достигает наибольшего значения 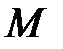 в некоторой точке
в некоторой точке  Это значит, что для любой точки
Это значит, что для любой точки  . Если
. Если 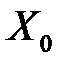 – угловая точка, то теорема доказана. Пусть
– угловая точка, то теорема доказана. Пусть 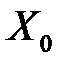 – не угловая точка, а угловыми являются точки
– не угловая точка, а угловыми являются точки 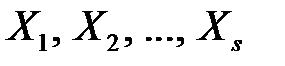 . Так как Ω – выпуклое множество, то для любой точки Х n-мерного пространства справедливо равенство:
. Так как Ω – выпуклое множество, то для любой точки Х n-мерного пространства справедливо равенство: 
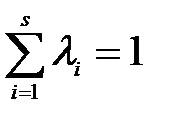 . Это равенство будет выполняться и для
. Это равенство будет выполняться и для 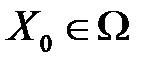 :
:
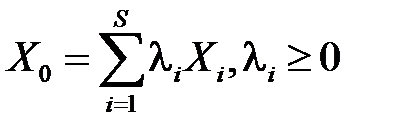 ,
, 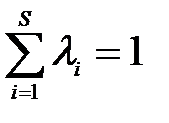 .
.
Так как функция  линейна, то
линейна, то 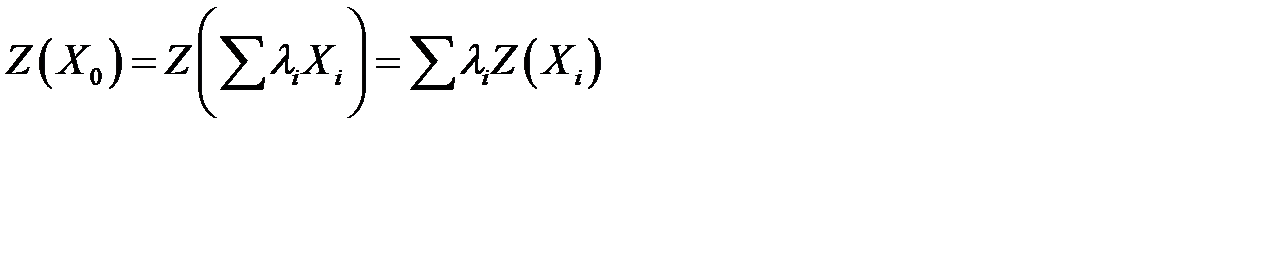 .
.
Обозначим через 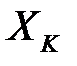 ту из вершин, в которой
ту из вершин, в которой  принимает наибольшее значение:
принимает наибольшее значение:  .
.
Тогда, 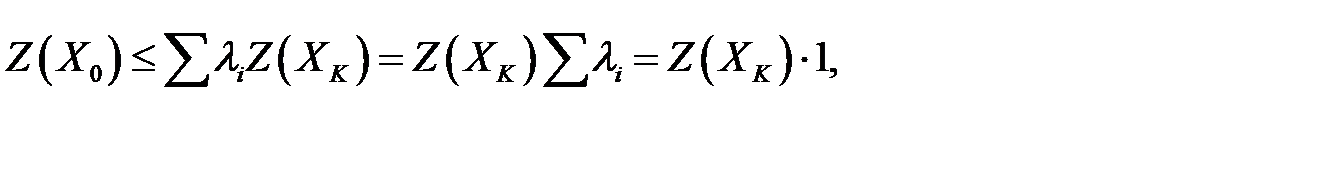 т. е.
т. е. 
Но по условию теоремы  поэтому это может быть если
поэтому это может быть если  . Следовательно,
. Следовательно,  , тогда
, тогда  , так как
, так как 
Предположим теперь, что  достигает в угловых точках
достигает в угловых точках 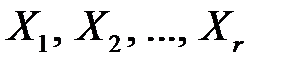 наибольшего значения, равного М, т. е.
наибольшего значения, равного М, т. е. 
Рассмотрим точку Х, являющуюся их линейной комбинацией:
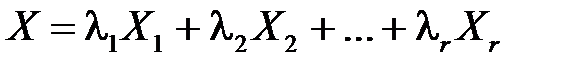 , (
, ( 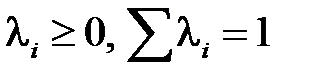 ).
).
Вычислим значение функции  в точке
в точке  :
:
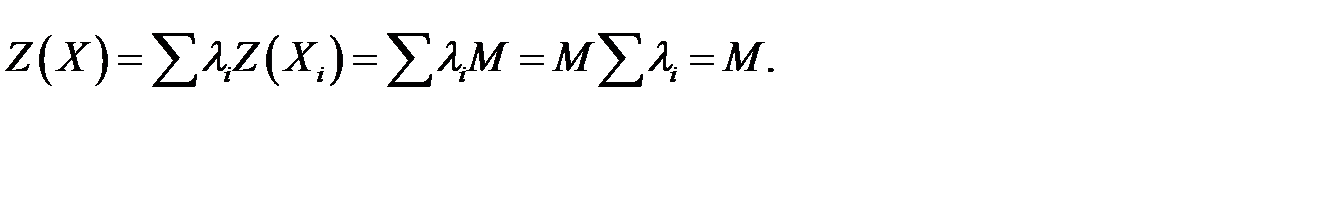
Значит, целевая функция достигает максимального значения в любой точке множества планов, являющихся линейной комбинацией крайних точек. Теорема доказана.
Геометрически это значит, что гиперплоскость, определяемая целевой функцией, отвечающая наибольшему значению 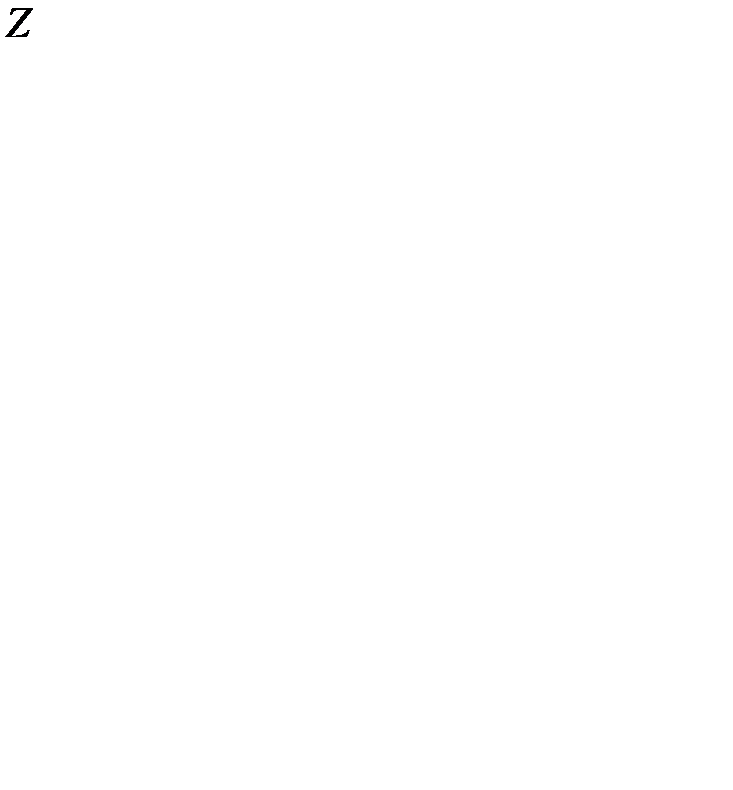 , проходит через угловую точку, либо через ребро, либо грань многогранника Ω, определяемого системой ограничений (1.16).
, проходит через угловую точку, либо через ребро, либо грань многогранника Ω, определяемого системой ограничений (1.16).
Так как угловой точке соответствует опорный план, то оптимальный план совпадает хотя бы с одним опорным планом линейнойоптимизационной модели. Следовательно, нужно проверить все опорные планы и выбрать тот, при котором 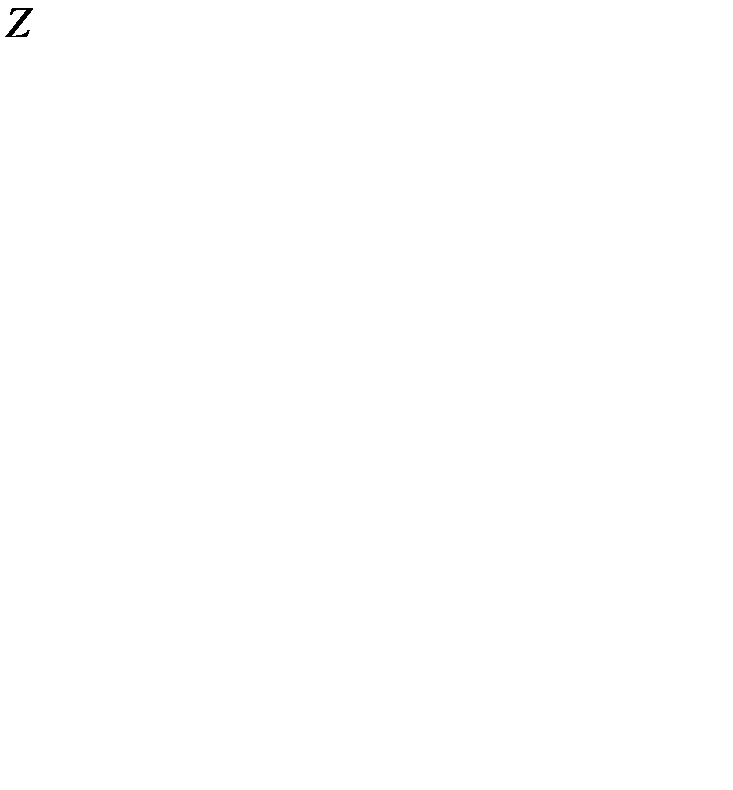 достигает оптимума. Но так как перебор всех опорных планов – процедура длительная, то разработаны методы упорядоченного перебора, позволяющие сократить число испытуемых опорных планов.
достигает оптимума. Но так как перебор всех опорных планов – процедура длительная, то разработаны методы упорядоченного перебора, позволяющие сократить число испытуемых опорных планов.
Лекция 2 Экономико-математические методы и модели оптимального планирования в промышленности, АПК (продолжение)
Вопросы, изучаемые на лекции:
2.1. Понятие о симплексном методе
2.2. Построение начального опорного плана
2.3. Признак оптимальности опорного плана
Дата добавления: 2015-09-29; просмотров: 845;
