Примеры линейных оптимизационных моделей
Пример 1.1. Линейная оптимизационная модель годовой производственной программы предприятия.
Производственная мощность предприятия характеризуется величиной годового максимально – возможного выпуска продукции при применении прогрессивных технологий, эффективной организации производства и наиболее полном использовании производственного оборудования предприятия. Математическая модель для определения производственной программы должна иметь критерий эффективности со стоимостными показателями продукции, хотя они имеют ряд недостатков (изменение цен на продукцию из-за инфляционных процессов, ставок оплаты труда, цен на сырье и др.)
Для построения модели введем обозначения:
· 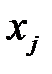 - объем производства продукции
- объем производства продукции  - го вида,
- го вида, 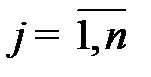 ;
;
· 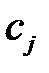 - стоимость единицы продукции
- стоимость единицы продукции  - го вида,
- го вида, 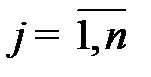 ;
;
· 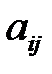 - время обработки
- время обработки  - ой продукции на
- ой продукции на 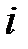 - том оборудовании;
- том оборудовании;
· 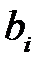 - фонд времени работы оборудования
- фонд времени работы оборудования 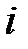 - го вида.
- го вида.
Математическая модель рассматриваемой задачи будет иметь вид:
Найти план 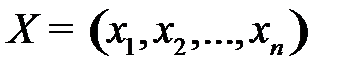 выпуска продукции, при котором предприятие получит максимум выручки
выпуска продукции, при котором предприятие получит максимум выручки
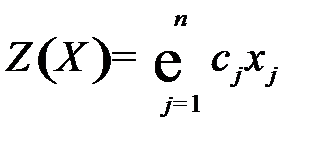
при ограничениях на фонд времени работы оборудования
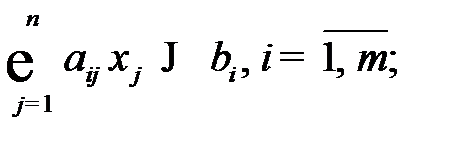
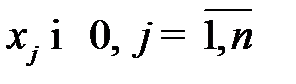 .
.
Частным случаем рассматриваемой модели является оптимизационная модель использования ресурсов.
Предположим, что предприятие может изготавливать четыре вида продукции 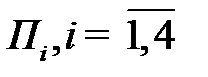 . Предприятие располагает ресурсами и нормами их расхода, приведенными в таблице 1.1
. Предприятие располагает ресурсами и нормами их расхода, приведенными в таблице 1.1
Таблица 1.1
| Ресурсы | Продукция | Объем ресурса | |||
| П-1 | П-2 | П-3 | П-4 | ||
| Трудовые ресурсы, человеко-смены | 2,5 | 2,5 | 1,5 | ||
| Полуфабрикаты, кг | |||||
| Станочное оборудование, станко-смены | |||||
| Прибыль от единицы продукции, ден. ед. |
Требуется: 1) определить план выпуска продукции, максимизирующей прибыль предприятия;
2) учесть требование комплектации, чтобы количество единиц третьей продукции было в два раза больше количества единиц первой;
3) определить оптимальный ассортимент при дополнительных условиях: первой продукции выпускать не менее 27 единиц, третьей – не более 35, а второй и четвертой – в отношении 2:3.
Построим математическую модель задачи. Для этого введем неизвестные величины  , характеризующие количество произведенной продукции. Критерий оптимальности – стоимостной (максимум прибыли предприятия). Следовательно, нужно определить план выпуска продукции
, характеризующие количество произведенной продукции. Критерий оптимальности – стоимостной (максимум прибыли предприятия). Следовательно, нужно определить план выпуска продукции 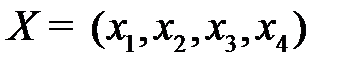 , при котором целевая функция
, при котором целевая функция 
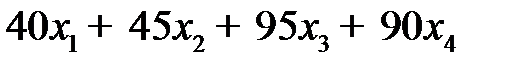 достигает максимального значения и который удовлетворяет системе ограничений:
достигает максимального значения и который удовлетворяет системе ограничений:
· на трудовые ресурсы: 
· на полуфабрикаты: 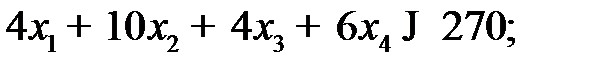
· на станочное оборудование: 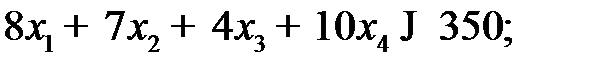
· условию неотрицательности переменных: 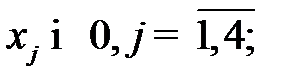
· дополнительное требование комплектации: 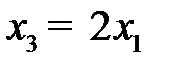 ;
;
· дополнительные условия: 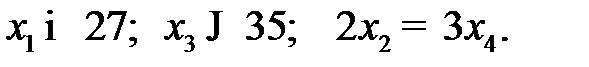
Линейная оптимизационная модель построена. Способы решения рассмотрим ниже.
Пример 1.2. Линейная оптимизационная модель о выборе технологий.
Предположим, что для выпуска некоторой однородной продукции можно использовать 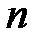 технологий и при этом используются
технологий и при этом используются 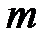 видов ресурсов, заданных соответственно объемами
видов ресурсов, заданных соответственно объемами 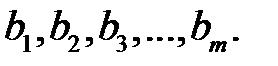
Построим математическую модель, решая которую определим оптимальную технологию для выпуска однородной продукции. Пусть: 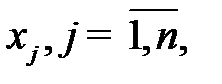 - время, в течение которого предприятие выпускает продукцию по
- время, в течение которого предприятие выпускает продукцию по  - тому технологическому способу;
- тому технологическому способу;
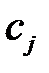 ,
, 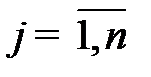 , - стоимость конечной продукции, производимой в единицу времени, по
, - стоимость конечной продукции, производимой в единицу времени, по  - тому технологическому способу;
- тому технологическому способу;
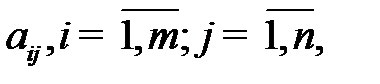 - расход
- расход 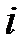 - го ресурса в единицу времени по
- го ресурса в единицу времени по  - тому технологическому способу.
- тому технологическому способу.
Пренебрегая временем переналадок, необходимым для перехода от одного технологического способа к другому, и воспользовавшись стоимостным критерием оптимальности, получим следующую математическую модель рассматриваемой задачи.
Определить оптимальное применение технологических способов 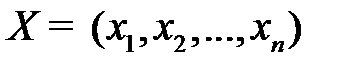 , при которых максимизируется объем выпуска ( в ден. ед.) продукции:
, при которых максимизируется объем выпуска ( в ден. ед.) продукции:

и, которые удовлетворяют системе ограничений:
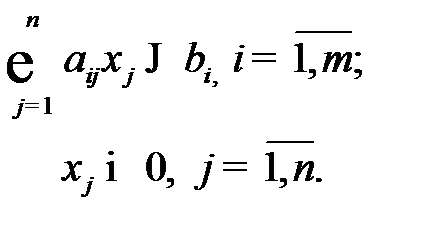
Предположим, что предприятие может работать по трем технологическим способам. Расход ресурсов за единицу времени при соответствующей технологии и производительность по каждому технологическому способу (в ден. ед.) в единицу времени, представим в таблице 1.2.
Таблица 1.2
| Ресурсы | Технологические способы | Объем ресурса | ||
| Т-1 | Т-2 | Т-3 | ||
| Трудовые ресурсы, человеко - часов | 1 300 | |||
| Сырье, т | ||||
| Электроэнергия, кВт/ч | 3 000 | |||
| Производительность технологического способа |
Определить план использования технологических способов, при котором максимизируется объем выпуска продукции.
Построим математическую модель задачи. Пусть  - время использования
- время использования  -го технологического способа. Требуется найти план
-го технологического способа. Требуется найти план 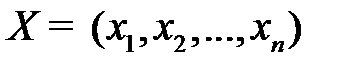 , при котором целевая функция
, при котором целевая функция

достигает максимального значения, и который удовлетворяет ограничениям:
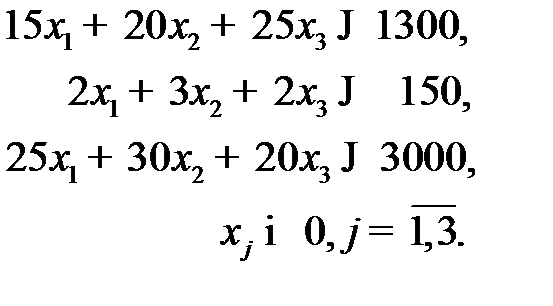
Пример 1.3.Линейная оптимизационная модель раскроя материалов.
На деревообрабатывающем предприятии листы фанеры для изготовления деталей изделий могут раскраиваться несколькими способами. Если лист раскроить по j-му способу раскроя ( 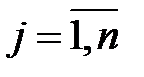 ), то получится
), то получится 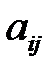 деталей i-го вида (
деталей i-го вида (  ), при этом отходы с одного листа равны
), при этом отходы с одного листа равны 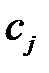 м2. Требуется найти, сколько листов фанеры раскраивать по каждому из способов раскроя, чтобы получить деталей i-го вида не менее
м2. Требуется найти, сколько листов фанеры раскраивать по каждому из способов раскроя, чтобы получить деталей i-го вида не менее 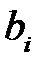 единиц, а количество отходов должно быть минимальным.
единиц, а количество отходов должно быть минимальным.
Составим математическую модель данной задачи.
Обозначим 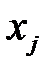 количество листов фанеры, раскраиваемых по j - тому способу. Определим план
количество листов фанеры, раскраиваемых по j - тому способу. Определим план 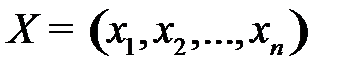 раскроя листов фанеры так, чтобы суммарное количество отходов по всем вариантам раскроя было минимальным:
раскроя листов фанеры так, чтобы суммарное количество отходов по всем вариантам раскроя было минимальным:

и чтобы выполнялись ограничения на изготовление деталей:

Количество листов фанеры, раскраиваемых по j - тому способу, должно быть неотрицательным:
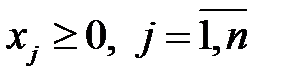 .
.
Пример 1.4. Линейная оптимизационная модель о рационе.
Сельскохозяйственное предприятие для откорма скота располагает n видами кормов (сочные, грубые, концентрированные и др.). Каждый вид корма характеризуется содержанием питательных веществ (кормовые единицы, белки, фосфор, кальций и др.). Известно содержание i-го питательного вещества в единице корма j-го вида и равно оно 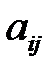 единиц (
единиц (  ,
, 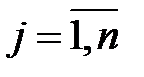 ), а также
), а также 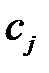 – стоимость единицы корма j-го вида (
– стоимость единицы корма j-го вида ( 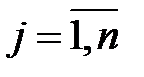 ) и минимальная суточная потребность скота в i-м питательном веществе
) и минимальная суточная потребность скота в i-м питательном веществе 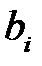 (
( 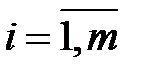 ). Требуется составить рацион минимальной стоимости.
). Требуется составить рацион минимальной стоимости.
Для построения математической модели данной задачи обозначим  - количество корма
- количество корма  - го вида. Определим рацион
- го вида. Определим рацион 
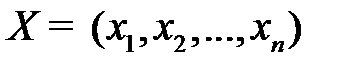 , при котором суммарная стоимость рациона:
, при котором суммарная стоимость рациона:

будет минимальной, а суточная потребность животного в питательном веществе 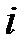 - го вида будет не менее минимального количества
- го вида будет не менее минимального количества 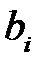 :
:

Количество корма, потребляемого животным, не может быть отрицательной величиной:
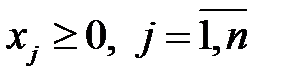 .
.
Пример 1.5. Линейная оптимизационная модель о назначениях.
Имеется n механизмов, которые могут использоваться для выполнения n работ. Известна производительность  каждого i-го механизма (
каждого i-го механизма ( 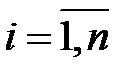 ). Требуется так закрепить механизмы за работами, чтобы суммарная их производительность была максимальной.
). Требуется так закрепить механизмы за работами, чтобы суммарная их производительность была максимальной.
Для составления математической модели задачи введем переменные:

Найдем план использования механизмов так, чтобы их суммарная производительность была максимальной:
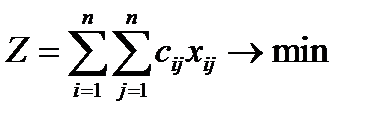 ,
,
при ограничениях:
· 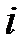 -ый механизм должен быть назначен только на одну работу:
-ый механизм должен быть назначен только на одну работу:
 ,
,
· каждая работа должна выполняться только одним механизмом:
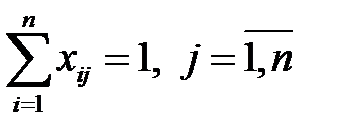 .
.
Пример 1.6. Линейная оптимизационная модель о размещениях.
Отраслью заключены договоры на поставку продукции потребителям в заданных ассортименте, объеме и сроках. Для выполнения договорных обязательств руководство отрасли разрабатывает мероприятия по расширению производства на ряде предприятий, проведению их реконструкции, а также строительству и вводу новых мощностей. Требуется определить объемы производства продукции на действующих, реконструируемых и вновь вводимых предприятиях, а также объемы поставок продукции от предприятий-поставщиков к потребителям, чтобы суммарные затраты на производство и доставку продукции были минимальными.
Введем обозначения и построим математическую модель задачи:
i – вид производимой продукции (  );
);
j – номер предприятия, производящего продукцию ( 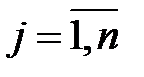 );
);
k – номер потребителя продукции ( 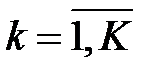 );
);
 – мощности j-го предприятия по производству продукции i-го вида;
– мощности j-го предприятия по производству продукции i-го вида;
 – стоимость производства единицы продукции i-го вида на j-м предприятии;
– стоимость производства единицы продукции i-го вида на j-м предприятии;
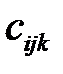 – затраты на перевозку единицы продукции i-го вида от j-го предприятия k-му потребителю;
– затраты на перевозку единицы продукции i-го вида от j-го предприятия k-му потребителю;
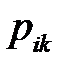 – объем поставки продукции i-го вида k-му потребителю согласно договорным обязательствам;
– объем поставки продукции i-го вида k-му потребителю согласно договорным обязательствам;
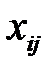 – искомый объем производства продукции i-го вида на k-м предприятии;
– искомый объем производства продукции i-го вида на k-м предприятии;
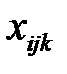 – объем поставки j-м предприятием продукции i-го вида k-му потребителю.
– объем поставки j-м предприятием продукции i-го вида k-му потребителю.
С учетом обозначений суммарные производственные и транспортные затраты в математической модели определяются следующим выражением
 .
.
Ограничения задачи:
· по мощностям каждого предприятия
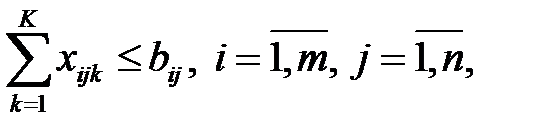
· по балансу производства и потребления продукции
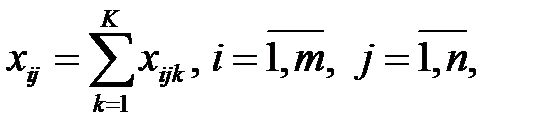
· по удовлетворению спроса потребителей
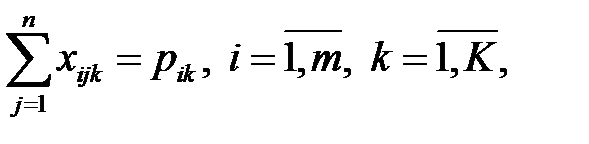
· объемы поставок и производства продукции должны быть неотрицательными:
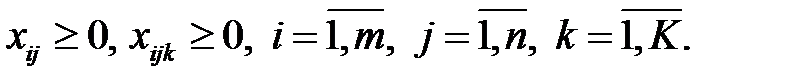
Дата добавления: 2015-09-29; просмотров: 1345;
