Экономико-математическое моделирование как средство для принятия эффективных решений
Предметом изучения дисциплины экономико-математические методы и модели являются количественные характеристики экономических процессов, протекающих в промышленном производстве, и их взаимосвязи. В курсе рассматриваются экономические задачи и их математические модели.
Под математической моделью понимается система математических соотношений (уравнений: алгебраических, дифференциальных, интегральных, в частных производных; графов; соотношений математической логики и др.) описывающих реальный объект, составляющие его характеристики и взаимосвязи между ними.
Таким образом, любая экономико-математическая модель выражает в математических соотношениях экономическую сущность условий задачи и поставленной цели исследования, т. е. экономические связи между экономическими параметрами или величинами описываются математическими соотношениями. Академик Немчинов писал: «Экономико-математическая модель представляет собой концентрированное выражение общих взаимосвязей и закономерностей экономического процесса в математической форме».
Классификация экономико-математических моделей условна и зависит от того, с использованием каких признаков строится модель. Так, например, экономико-математические модели можно подразделить на: статистические, балансовые и оптимизационные.
Статистические – это модели, в которых описываются корреляционно-регрессионные зависимости результата производства от одного или нескольких независимых факторов. Эти модели широко используются для построения производственных функций, а также при анализе экономических систем.
Балансовые модели представляют систему балансов производства и распределения продукции и записываются в форме квадратных матриц. Балансовые модели служат для установления пропорций и взаимосвязей при планировании различных отраслей народного хозяйства.
Оптимизационные модели представляют систему математических уравнений, линейных или нелинейных, подчиненных определенной целевой функции и служащих для отыскания оптимальных (наилучших) решений экономической задачи. Эти модели описывают условия функционирования экономических систем.
Оптимизационные и балансовые экономико-математические модели содержат систему ограничений и целевую функцию.
Система ограничений состоит из отдельных математических уравнений или неравенств, называемых балансовыми уравнениями или неравенствами. Целевая функция связывает между собой различные величины моделей. Это функция многих переменных. В качестве цели, как правило, выбирается экономический показатель: прибыль, рентабельность, себестоимость, объем валовой продукции и т. д.
Критерий оптимальности – это также экономический показатель, выражающийся при помощи целевой функции через другие экономические показатели. Одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Критерии оптимальности могут быть натуральные и стоимостные. Одни из критериев – максимизирующие (например, максимизировать прибыль предприятия, рентабельность), другие – минимизирующие (например, минимизировать затраты труда при производстве продукции).
Решением экономико-математической модели или допустимым планом называется набор значений неизвестных, удовлетворяющих системе ограничений. Модель имеет бесконечное множество решений (или допустимых планов) и среди них нужно найти единственное, удовлетворяющее системе ограничений и целевой функции.
Допустимый план, удовлетворяющий целевой функции, называется оптимальным. Он, как правило, единственный.
Отметим, что если модель имеет множество оптимальных планов, то для каждого из них значение целевой функции одно и то же.
Таким образом, для нахождения наилучшего оптимального экономического решения любой экономической задачи, необходимо построить ее математическую модель, структура, которой содержит систему ограничений, целевую функцию, критерий оптимальности, и решить ее методами математической обработки данных.
Для построения математической модели в первую очередь определяется система переменных величин: 
Переменные могут иметь один индекс 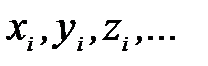 или несколько индексов
или несколько индексов 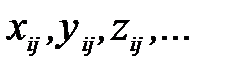 По каждой переменной для конкретной модели дается пояснение. Затем вводится целевая функция – цель задачи – обозначаемая
По каждой переменной для конкретной модели дается пояснение. Затем вводится целевая функция – цель задачи – обозначаемая  ,
, 
Постоянные величины обозначаются - 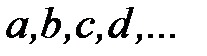 Они также могут иметь индексы: один -
Они также могут иметь индексы: один - 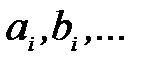 , или несколько индексов:
, или несколько индексов:  .
.
Далее составляются основные (все учесть невозможно) ограничения, которые отражают все условия, формирующие оптимальный план.
В построенной, таким образом, экономико-математической модели воспроизводятся лишь основные, наиболее важные в данном исследовании, стороны изучаемого объекта. Поэтому моделирование позволяет выявить существенные факторы, ответственные за те или иные свойства изучаемых явлений.
Следует отметить, что большинство экономико-математических моделей сводится к задачам линейного или нелинейного программирования, и такие модели могут быть представлены в общей, симметричной или канонической форме записи.
Лекция 1 Экономико-математические методы и модели оптимального планирования в промышленности, АПК
Вопросы, изучаемые на лекции:
1.1. Оптимальное планирование деятельности промышленных и сельскохозяйственных предприятий. Линейные оптимизационные модели
1.2. Примеры линейных оптимизационных моделей
1.3. Графический способ решения линейных оптимизационных моделей
1.4. Свойства решений линейной оптимизационной модели
Оптимальное планирование деятельности промышленных и сельскохозяйственных предприятий. Линейные оптимизационные модели
Оптимизационные модели представляют систему математических уравнений, линейных или нелинейных, подчиненных определенной целевой функции и служащих для отыскания наилучших (оптимальных) решений конкретной экономической задачи. Эти модели относятся к классу экстремальных задач и описывают условия функционирования экономической системы.
Оптимизационные модели могут носить детерминированный или стохастический характер. В детерминированных моделях результат решения однозначно зависит от входных данных. Стохастические модели описывают случайные процессы, в которых результат всегда остается неопределенным.
Наиболее разработаны и практически более применимы детерминированные модели, использующие аппарат математического программирования.
Структура оптимизационной модели состоит из целевой функции, принимающей значения в пределах ограниченной условиями задачи области, и из ограничений, характеризующих эти условия.
В общем виде оптимизационную математическую модель можно представить в следующем виде:
Найти план 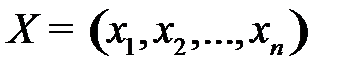 , который max (min) целевую функцию
, который max (min) целевую функцию
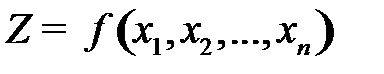 (1.1)
(1.1)
при выполнении ограничений
 (1.2)
(1.2)
где 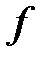 и
и 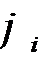 - известные функции,
- известные функции, 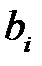 - заданные постоянные величины.
- заданные постоянные величины.
Вид целевой функции 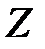 , вид ограничений и специальные ограничения на переменные (например, требования целочисленности переменных) определяют выбор метода математического программирования для решения оптимизационной задачи:
, вид ограничений и специальные ограничения на переменные (например, требования целочисленности переменных) определяют выбор метода математического программирования для решения оптимизационной задачи:
· линейного программирования;
· нелинейного программирования;
· динамического программирования;
· целочисленного программирования и т. д.
Мы остановимся на оптимизационных моделях, которые решаются методами линейного программирования, т. е. рассмотрим оптимизационные модели (1.1) - (1.2) у которых целевая функция 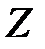 и ограничения
и ограничения 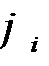 - линейные функции. Тогда оптимизационная математическая модель примет вид:
- линейные функции. Тогда оптимизационная математическая модель примет вид:
Найти план 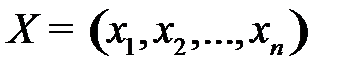 , который max (min) целевую функцию
, который max (min) целевую функцию
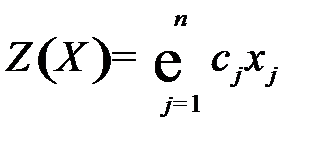 (1.3)
(1.3)
при выполнении системы ограничений
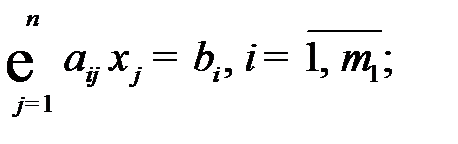 (1.4)
(1.4)
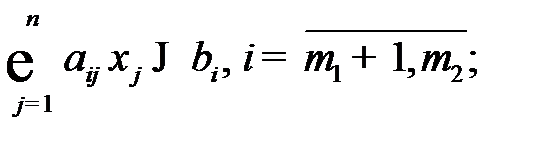 (1.5)
(1.5)
 (1.6)
(1.6)
 (1.7)
(1.7)
Множество планов 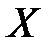 , удовлетворяющих системе ограничений (1.4) – (1.7), называется множеством допустимых решений и обозначается
, удовлетворяющих системе ограничений (1.4) – (1.7), называется множеством допустимых решений и обозначается 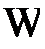 . Допустимый план
. Допустимый план  , доставляющий целевой функции (1.3) экстремальное значение, называется оптимальным.
, доставляющий целевой функции (1.3) экстремальное значение, называется оптимальным.
Отметим, что максимизация целевой функции 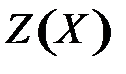 в области допустимых решений
в области допустимых решений 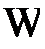 эквивалентна задаче минимизации функции «
эквивалентна задаче минимизации функции « 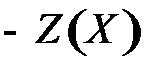 » в той же области:
» в той же области:  .
.
Если все ограничения задачи заданы в виде равенств и на все переменные 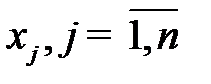 , наложено условие неотрицательности
, наложено условие неотрицательности 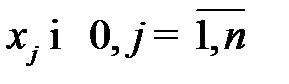 , то оптимизационная модель имеет каноническую форму записи:
, то оптимизационная модель имеет каноническую форму записи:
max 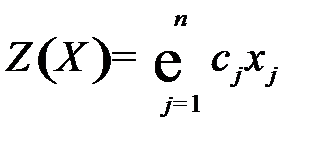
при ограничениях
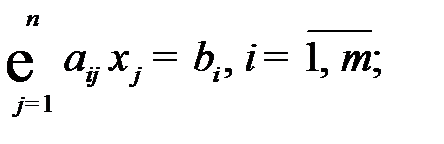
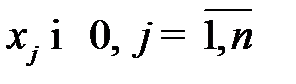 .
.
Если ограничения заданы в виде неравенств, то оптимизационная модель имеет симметрическую форму записи:
max 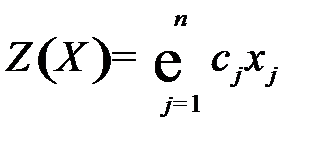
при ограничениях
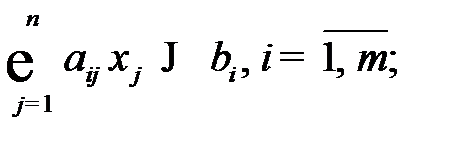
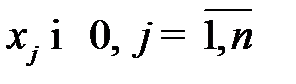 ,
,
или
min 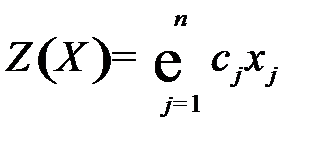
при ограничениях

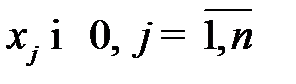 .
.
Для аналитического решения линейной оптимизационной модели, в случае необходимости, ее ограничения следует преобразовать к каноническому виду, для чего переходят от ограничений неравенств к равенствам, введением дополнительных переменных  , которые прибавляют к левым частям ограничений неравенств. В целевую функцию дополнительные переменные вводятся с коэффициентами равными нулю.
, которые прибавляют к левым частям ограничений неравенств. В целевую функцию дополнительные переменные вводятся с коэффициентами равными нулю.
Дата добавления: 2015-09-29; просмотров: 2469;
