Методы дихотомии и золотого сечения

Метод дихотомии

Метод дихотомии применяется для унимодальных функций. Метод дихотомии заключается в том, что исходный интервал [а,b] делится средней точкой на два подинтервала [а,с] и [с,b] в одном из которых лежит точка минимума .

Для выбора подинтервала, для хорошо дифференцируемой функции вычисляют в точке c производную 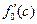и анализируют ее знак. Если 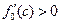, то лежит слева от точки c, т.е. В отрезке [а,с]; если 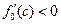, то лежит справа от точки c, т.е. В отрезке [с,b], а при найдена точка минимума .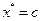

Если 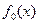не дифференцируемая, то выясняется направление убывания унимодальной функции. С этой целью задается точка с+h (где h>0 − малая величина, соизмеримая с ε и вычисляется ордината f₀(с+h).

Если приращение функции 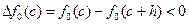, то точка лежит справа от точки c, т.е. принадлежит отрезку [с,b].

Если 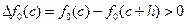, то точка лежит сktdf от точки c, т.е. принадлежит отрезку [a,c].

При 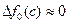имеем точку минимума .

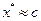После выбора подинтервала, в котором находится , например [с,b], переопределяем левую границу а=с (при выборе [а,с] следует поменять правую границу b=с).

Проверяем 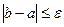, если нет, то вновь делим отрезок [b-a] пополам и опять определяем, в каком подинтервале находится точка минимума.

Алгоритм поиска минимума:

1. Вводим границы [а,b] и ε. h = 100⋅ε.

2. Делим отрезок пополам с = (b+a)/2.

3. Вычисляем приращение функции 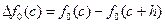. Если 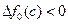, то a=с, иначе если 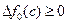, то b=с.

4. Проверяем условие 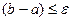? Если нет, то переходим на п.2, да – переход на п.5.

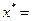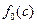5. Печать: "точка минимума ", с, , . Конец.

Для контроля правильности полученного решения можно вывести на печать значение 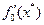, которое должно быть близко к нулю. Если 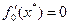не выполняется, то следует искать ошибку в программе.

Если интервал, содержащий точку минимума функции определяется на основе вычисления производной , то такая реализации метода дихотомии будет относиться к итерационным процедурам 1 порядка.