Выпуклые задачи оптимизации

Постановка задачи

Выпуклой задачей (или задачей выпуклого программирования) называется следующая задача оптимизации:

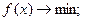
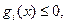
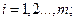
(36.1)

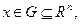
где 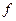, , 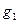,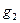...., 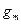– выпуклые функции, заданные на выпуклом и замкнутом множестве G .

Точка х, принадлежащая множеству G и удовлетворяющая неравенствам 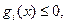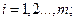. называется допустимой в задаче (36.1).

Если функция f определена и выпукла на выпуклом множестве 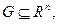то в выпуклой задаче локальный минимум является и глобальным.

Пусть х – точка локального минимума функции 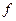, т.е. такое, что

Возьмем произвольную фиксированную точку 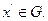Из условия выпуклости множества G следует, что точка

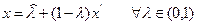
принадлежит множеству G.

При

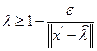
где

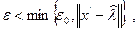
получаем

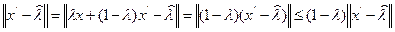
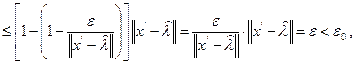
что означает

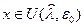
и, следовательно,

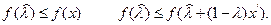
По условию функция 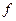выпукла. Поэтому последнее неравенство примет вид

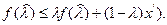
В частности, при

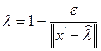
имеем

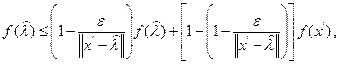
Отсюда

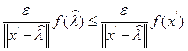
или

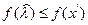
Так как 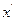– произвольная точка множества 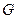, то из последнего неравенства следует, что 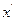– точка глобального минимума функции 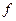на .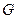

В дальнейшем в выпуклых задачах оптимизации, говоря "минимум", будем, подразумевать глобальный минимум.