Метод тяжелого шарика
Для поиска глобального минимума невыпуклой функции, которая имеет "неглубокие" локальные минимумы, находят применение многошаговые методы, использующие на k-й итерации значения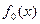 
.
Идея использования метода "тяжелого шарика" и его названия основаны на физической интерпретации процесса качения шарика по наклонной поверхности. Если шарик тяжелый, то он будет проскакивать мелкие впадины по инерции. Чем больше масса шарика, тем глубже будет впадина, в которой он остановится.
Двухшаговая итерационная процедура поиска глобального минимума 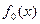методом "тяжелого шарика" имеет следующий вид
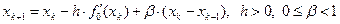, (35.1)
где k – номер итерации (k=1,2,...,). h, β параметры, которые подбираются в процессе решения задачи.
Скорость приближения {xk} к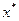 
зависит не только от "крутизны" функции в точке xk, характеризуемой величиной 
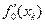, но и от "инерции" последовательности {xk}, которая пропорциональна слагаемому. При попадании точки 
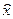в локальный минимум производная 
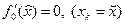, но инерционная составляющая при этом должна отличатся от нуля, поэтому
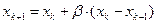
и последовательность {xk} продолжит движение к 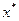. Подобная особенность итерационного метода "тяжелого шарика" позволяет "проскакивать" по инерции мелкие, неглубокие локальные минимумы и останавливаться в точках глобального экстремума. Окончание процесса итерации
.
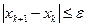Алгоритм поиска минимума методом тяжелого шарика:
1. Вводим два приближения х0 и х1, вычисляем значения критерия
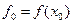и 
.
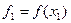2. Вычисляем значение производной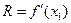 
.
3. Вычисляем предполагаемую точку минимума х по формуле
.
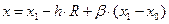4. Вычисляем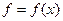 
. Проверяем условие улучшаемости 
?
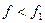"Да" – проверяем условие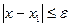 
, если выполняется, то переходим на п.6, иначе − на п.5; нет – за точку минимума принимаем точку х1, то есть х = х1 и переходим на п.6, либо можно изменить параметры h или β и продолжить поиск минимума в окрестности точки х1.
5. Переопределяем точки х0 = х1; х1 = х и переходим на п.2.
6. Печать "х*= ", х, оптимального значения критерия 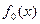, для контроля правильности полученных данных – 
.
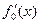Блок-схема рассмотренного метода приведена на рис.35.1(а,б). В алгоритме предусмотрен выбор параметров в процессе решения задачи на ЭВМ. При величине шага меньшей заданной точности выполняется переход на п.6. Критерий цели и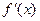 
заданы функциями пользователя f и pr соответственно.
Рис.35.1а. Блок-схема поиска минимума методом тяжелого шарика
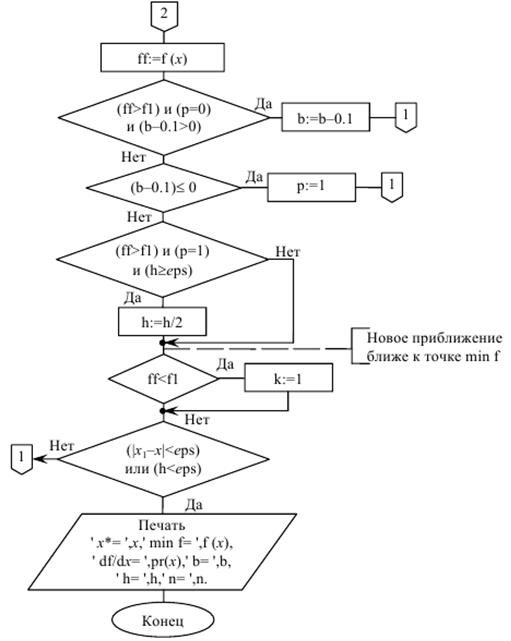
Рис.35.1б. Продолжение блок-схемы поиска минимума
методом тяжелого шарика
Лекция №36
Дата добавления: 2015-11-06; просмотров: 3363;