Методы квадратичной интерполяции и полиномиальной аппроксимации

Методы квадратичной интерполяции

Метод квадратичной интерполяции используют для поиска точки минимума 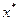непрерывной функции f(x), определенной на множестве 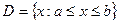. Из области допустимых значений D выделяется подмножество D₁, в котором расположена точка экстремума 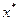, и аппроксимируется функция f(x) (х принадлежит подмножеству D₁) некоторой сильно выпуклой функцией вида:

.

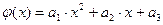Далее аналитическим методом находится точка минимума x₄ функции 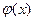из необходимого условия существования экстремума

.

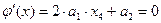Отсюда

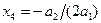, (34.1)

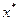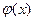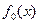которая тем ближе к точке , чем ближе функция к на подмножестве D₁.

Для нахождения множества D и коэффициентов a, b, c функции 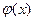необходимо подобрать вблизи предполагаемого минимума x₄ точки x₁, x₂, x₃, такие, что крайние ординаты больше средней ординаты, т.е. при x₁<x₂<x₃ было справедливо неравенство:

.

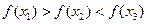По условию интерполяции значения аппроксимирующей параболы 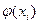должны совпадать со значениями целевой функции 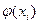, 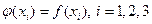. В результате получается система линейных уравнений, относительно неизвестных коэффициентов :

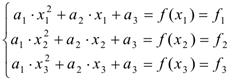
Далее находятся неизвестные коэффициенты по методу Крамера:

(34.2)

где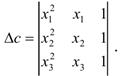

С учетом соотношений (34.1) и (34.2) получается выражение для определения точки x4 непосредственно через x_i, f_i,(i=1,2,3):

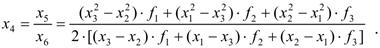(34.3)

Следует заметить, что в (34.3) знаменатель x₆ должен быть отличен от нуля. Если точки x₁, x₂, x₃, близки друг к другу, то это условие нарушается.