Лексикографическая оптимизация
Критерии упорядочиваются по относительной важности. Упорядочим критерии, например, следующим образом: З > Д > В.
Максимальное значение по критерию З в табл. 4.2 имеют альтернативы 3 и 7 (таблица 4.5):
| Таблица 4.5 – Сужение множества Мп | |||
| Альтер-нативы | Критерий | ||
| З (руб.) | Д (дни) | В (мин.) | |
| -40 | |||
| -60 |
По второму по значимости критерию оптимальной будет альтернатива 7.
Основные недостатки подхода — трудности в полной упорядоченности критериев по их важности и фактический учёт только одного критерия. На первом шаге отбираются исходы, имеющие максимальную оценку по важнейшему критерию. Второй критерий учитывается, только тогда, если по важнейшему критерию максимальную оценку имеют более одного исхода.
3.3.4. Линейная свёртка
Построение обобщённого критерия или метод линейной свёртки — это взвешенная сумма частных критериев, которая превращает векторную оценку d = (d1, d2, …, dk) в скалярную:
j(d) = a1∙d1 + a2∙d2 + … + ak∙dk, где aj ³ 0, j = 1, …, k, 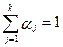 .
.
Числа aj называют весовыми коэффициентами, j = 1, …, k. Величина коэффициента aj показывает относительную важность j-го критерия.
Недостаток — субъективизм при выборе весовых коэффициентов.
В нашем примере d = (d1, d2, d3).
j(d) = a1∙d1 + a2∙d2 + a3∙d3, где aj ³ 0, j = 1, 2, 3.
Примем следующие значения критериев: a1 = 0.6, a2∙= 0.2, a3∙= 0.2.
Так как значения критериев измеряются в разных шкалах, то проведём процедуру квантификации, т.е. введём для них единую систему оценки. Для каждого критерия введём градации в баллах от 1 до 9. Пусть получены следующие оценки значений критериев.
Зарплата З (руб.): 14000 ¸ 16000 — 4 балла.
16001 ¸ 18000 — 6 баллов.
18001 ¸ 20000 — 8 баллов.
Длительность отпуска Д (дни): 30 ¸ 40 — 4 балла.
41 ¸ 50 — 6 баллов.
51 ¸ 60 — 8 баллов.
Время поездки на работу В (минуты): -60 ¸ -50 — 9 баллов.
-49 ¸ -40 — 7 баллов.
-39 ¸ -30 — 5 баллов.
-29 ¸ -20 — 3 балла.
-19 ¸ -10 — 1 балл.
Таблица 4.2 будет преобразована в таблицу. 4.6:
| Таблица 4.6 – Процедура квантификации | |||
| Альтер-нативы | Критерий | ||
| З (руб.) | Д (дни) | В (мин.) | |
Вычислим скалярные оценки альтернатив:
3: j(d) = 0.6×8 + 0.2×4 – 0.2×7 = 4.8 + 0.8 – 1.4 = 4.2
4: j(d) = 0.6×6 + 0.2×4 – 0.2×9 = 3.6 + 0.8 – 1.8 = 2.6
5: j(d) = 0.6×4 + 0.2×8 – 0.2×1 = 2.4 + 1.6 – 0.2 = 3.8
6: j(d) = 0.6×4 + 0.2×4 – 0.2×1 = 2.4 + 0.8 – 0.2 = 3.0
7: j(d) = 0.6×8 + 0.2×4 – 0.2×9 = 4.8 + 0.8 – 1.8 = 3.8
Оптимальной будет альтернатива 3.
Дата добавления: 2015-11-10; просмотров: 2227;
