Аналогичное моделирование

Аналогичное моделирование - замещение оригинала аналогичной моделью, обладающей сходством с оригиналом, достаточным для экстраполяции ее свойств и отношений в свойства и отношения оригинала на основании умозаключений по аналогии. Аналогичное моделирование используется обычно при сравнительно слабой изученности оригинала, когда имеющиеся сведения об его свойствах носят только качественный характер.

Вывод: при удачном выборе модели аналогичное моделирование позволяет получить весьма интересные и важные результаты. К сожалению, общая методика аналогичного моделирования невозможна, и требуется поиск модели. Во многих случаях целесообразно использовать аналогичные формальные модели, основанные на механических, электрических, акустических аналогиях.

Элементы теории подобия

Понятие подобия

Особое место среди математических моделей занимают подобные. Если при аналогии двух объектов распространение свойств одного объекта на другой носит характер предположения и нуждается в проверке, то при подобии знание свойств одного объекта значит знание свойств другого объекта.

Подобие - это полная математическая аналогия при наличии пропорциональности между сходственными переменными, неизменно сохраняющаяся при всех возможных значениях этих переменных, удовлетворяющих сходственным уравнениям.

Впервые понятие «подобие» появилось в геометрии.

Геометрическое подобие – определяют подобность геометрических фигур по сходственным характеристикам. Многоугольник с определенным количеством сторон n, подобен другому многоугольнику с таким же количеством сторон n, если соответствующие углы многоугольников равны, а соответствующие стороны пропорциональны. Определение геометрического подобия многоугольников, на примере треугольников, состоит в следующем:

треугольники подобны, если у них сходственные стороны пропорциональны, а сходственные углы равны и, т. е. выполняются следующие равенства:

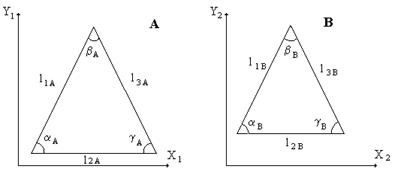
Рис.5 Подобие треугольников

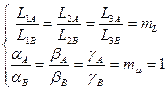, (1)

где m_L и m_m - масштабные коэффициенты (масштабы) величин сторон и углов, характеризующие пропорциональность сходственных параметров.

(Оговорка: если m_L и m_m называются масштабными коэффициентами, то величины обратные им , т.е. 1/m_L и 1/m_m будут называться масштабами и обозначаться, соответственно, M_L и M_m или наоборот, или вообще не делается различия между терминами «масштаб» и «масштабный коэффициент»).

На практике при геометрическом подобии используются не характеристики длин сторон многоугольника, а их координаты.

Если ввести систему прямоугольных координат X, Y, то при геометрическом подобии все координаты x_iA, y_iA первого многоугольника пропорциональны соответствующим координатам x_iB, y_iB второго многоугольника, т.е. выполняются соотношения

x_iA, / x_iB =m_x; y_iA / y_iB = m_y; m_x = m_y,

где x_i и y_i координаты любой точки, находящейся на отрезках прямых, определяющих контуры соответствующего многоугольника; m_x и m_y - масштабы.

Данный вид подобия может существовать и в пространстве большей размерности: трех - и более мерном.

Дальнейшее развитие понятия подобие является - аффинное подобие, при котором допускается неравенство масштабов по отдельным координатным осям.

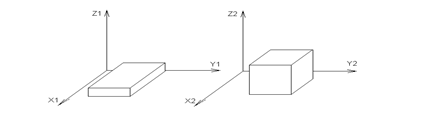
Рис.6 Превращение параллелепипеда в куб.

При аффинном подобии для сходственных точек в трехмерном координатном пространстве будут справедливы следующие соотношения:

x_iA / x_iB = m_x; y_iA / y_iB = m_y; z_iA / z_iB = m_z; m_x¹ m_y ¹ m_z.

При этом требуется введения специальных преобразующих функций, осуществляющих взаимосвязь между координатами моделей и объекта, часто - нелинейных.

Пример: установить условия аффинного подобия на рис. 4, отрезки линий e₁ - l₁ являются не линейно сходственными линиями e₂ - l₂, точки e₁, f₁, g₁, h₁, i₁ соответствуют точкам e₂, f₂, g₂, h₂, i₂.

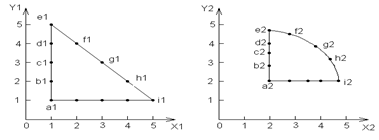
Рис.7 Нелинейное преобразование

Уравнения для контуров e₁ - i₁ и e₂ - i₂ имеет вид:

x₁ + y₁ = 6; x₂² + y₂² = 24.

Вводятся масштабные коэффициенты F_x = x₁ / X₁ и F_y = y₁ / Y₁, вид которых пока неизвестен, для уравнения первого контура можно записать:

X₁ F_x + Y₁ F_y = 6,

где X₁ и Y₁ преобразованные в область B значения x₁ и y₁ из области A. После тождественных преобразований уравнение выглядит:

[(2X₁ / Ö x₁) F_x]² + [(2Y₁ / Ö y₁) F_y]² = 24,

таким образом F_x = Ö x₁ / 2; F_y = Ö y₁ / 2 и, следовательно :

x₂ = 2Ö x₁ и y₂ = 2Ö y_1.

В приведенном примере функции преобразования F_x и F_y имеют одинаковый вид, но нелинейный характер.

Следующий пример: даны две сходственные функции: 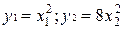, если масштабы m_y = y₁ / y₂: m_x = x₁ /x₂, соответственно равны 2 и 4, то функции подобны.

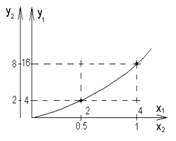
Рис.8 Подобные функции (пример)

В этом примере переменные имеют различные масштабные коэффициенты по координатным осям.

Пример. Имеются два генератора переменного тока. Их описывает функция зависимости напряжения от времен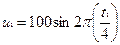и: и 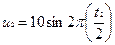. Выражения для масштабов имеют вид m_u = u₁ / u₂, m_t = t₁ / t₂. Время, входящее в одну формулу и время, входящее в другую формулу имеют вполне определенный физический смысл, так как t₁ и t₂ такие различные значения одной и то же величины t, при которых фиксируются значения различных зависимых переменных u₁(t) и u2(t).

Физическое и временное подобие имеет место при m_u = 10 и m_t = 2. Масштаб m_u показывает отношение амплитуд напряжений u₁ и u₂, масштаб m_t - отношение периодов T₁ = 4c и T₂ = 2c.

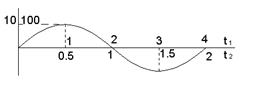
Рис.9 Подобие генераторов (пример)

В общем случае временного подобия безразмерный масштаб времени представляет отношение сходственных временных интервалов, которым соответствует неизменное отношение значений или приращений подобных временных функций. Этими параметрами могут быть периоды колебаний (как в примере), постоянные времени, длительности переходных процессов, временные задержки и т.д.

Если, например, имеются две подобные САУ, то, установив время переходного процесса одной из них t₁ и зная временной масштаб m_t, можно найти время переходного процесса другой системы: t₂ = t₁ / m_t.