Условное моделирование
Условное моделирование - это замещение оригинала условной моделью, представляющей его только благодаря договоренности о смысле, приписанном этой модели. Прежде всего - знаковые модели. Знак или символ - искусственный образ, чисто условно изображающий вполне определенный объект и, как правило, не имеющий с этим объектом никакого сходства. Отдельный знак (т.е. простейшая условная модель) обладает ограниченными моделирующими возможностями. Он условно обозначает вещь, явление, действие, событие, свойство, связь или отношение вещей, явлений, свойств и т.д. Однако, в случае применения системы знаков, эти возможности резко возрастают.
Сформулировать общие правила построения знаковых моделей невозможно, так как формирование их имеет поисковый эвристический характер.
Основные требования, предъявляемые к таким моделям:
* необходимость - невозможность использовать имеющиеся символы;
* простота - простое при равных условиях предпочтительнее сложного;
* наглядность - хотя бы самое отдаленное сходство с оригиналом;
* индивидуальность - достаточное отличие от других символов;
* однозначность - недопустимость обозначения одним символом различных объектов;
* единообразие - при моделировании однородных объектов;
* определенность - сопровождение четким указанием о принятом решении;
* учет установившихся традиций.
Пример: запись кубического уравнения вида Дx3 + xx2 + Ox + Á = 0 явно неудачна. Более удачно Ax3 + Bx2 + Cx + D = 0, еще лучше A0x3 + A1x2 + A2x + A3 = 0, самая удачная A3x3 + A2x2 + A1x + A0 = 0, которую легко записать в сокращенной форме 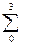 Aixi = 0.
Aixi = 0.
Если знаковая модель выбрана удачно, она получает всеобщее признание, примером этого служат русские и латинские буквы, примерами неудачных - немецкие готические и иероглифы.
Условными являются также образно-знаковые модели, которые отличаются наглядностью и могут обладать определенным сходством с оригиналом. Например, структурные схемы, направленные графы систем автоматизированного управления наглядно показывают число звеньев, связи звеньев, переменные величины, действующие на входах и выходах звеньев и системы в целом.
К знаковым и образно-знаковым моделям относятся все математические формы выражения количественных отношений между переменными и постоянными величинами (функции, уравнения, неравенства, графики, номограммы, таблицы, алгоритмы и т.д.).
Практически при применении математических методов приходится иметь дело с математическим описанием материальных объектов, являющимися условными логическими моделями количественных отношений между размерами и числовыми значениями физических величин.
В общем случае физическая величина Х - это некоторое свойство материального объекта, допускающее количественное выражение, например, длина L, объем V, масса M, вообще.
Количественное значение физической величины Х в конкретном материальном объекте х - это размер физической величины Х.
Для определения размера х физической величины Х данного объекта требуется сравнить ее размер с размером {x} той же физической величины другого объекта, принятого за единицу.
В результате измерения устанавливается числовое значение х° размера х:
х° = х / {x} (1.1)
и размер выражается через числовое значение х° и единицу измерения {x}:
х = х°{x} (1.2)
Символы х, х°, {x} в формуле (2) как условной знаковой модели моделируют размер, числовое значение и единицу физической величины Х. Знак = означает равенство объектов - оригиналов, символические модели которых расположены справа и слева от него. Эти символы называются членами формулы.
Размер х не зависит от единицы измерения {x}, от нее зависит только числовое значение х° размера х.
Каждый материальный объект обладает несколькими свойствами, допускающими количественное выражение. Между различными свойствами объективно существуют конкретные связи. Они обуславливают определенные соотношения между размерами физических величин, которые можно выразить в виде формулы. Поэтому, если выбрать произвольно единицы некоторых физических величин, то через эти единицы можно выразить единицы всех остальных физических величин.
Основные физические величины - размеры единиц, которых выбираются произвольно. Единицы измерения основных физических величин также называются основными.
Производные единицы измерения - единицы измерения остальных физических величин, которые выражены через основные на основе физических законов между величинами исходного объекта величинами и величинами единиц измерения, которые приняты в качестве основных.
[u] = [L][T-1] F = am[F] = [L][T-2][M]
Система единиц измерения - совокупность основных и производных единиц.
В системе «СИ» основные физические величины - длина, масса, время, сила электрического тока, сила света, количество вещества, температура. Основные единицы этой системы - метр (м), килограмм (кг), секунда (с), ампер (А), кандела (кд), моль (моль), кельвин (К).
Пусть для физических величин Y1, Y2,... выбраны независимые основные единицы {y1}, {y2},... и для другой величины X требуется установить производную единицу {x}. Для этого выбирается материальный объект, в котором размеры X, Y1, Y2,... связаны уравнением:
x = k F(y1, y2,...), (1.3)
где k - коэффициент пропорциональности, или
x° {x} = k F(y1°{y1}, y2{y2}, ...) (1.4)
Положив x° = y1° = y2° = ... = 1, можно выразить производную единицу через основные:
{x} = k F({y1}, {y2},...). (1.5)
Для обеспечения идентичности выражений, размеры и числовые значения X, Y1, Y2 ,..., аналогичной (3) должна быть зависимость:
x° = k F( y1°, y2°,...). (1.6)
Подставляя выражения (5), (6) в (4) получим:
k F( y1°, y2°,...) k F({y1}, {y2},...) = k F(y1°{y1}, y2°{y2}, ...),
равносильное системе двух уравнений:
k2 = k, (1.7)
F(y1°{y1}, y2°{y2}, ...) = F( y1°, y2°,...) F({y1}, {y2},...) (1.8)
Алгебраическое уравнение (7) имеет два корня (0, 1), смысл имеет k = 1. Выражение (7) функциональное, в котором неизвестен вид функции F. По смыслу выражения (3) эта функция должна быть непрерывной, единственной функцией удовлетворяющей условию (7) является произведение степеней y1, y2, ..., т.е. функция:
F(y1, y2, ... ) = y1a1 y2a2 ... , (1.9)
в которой показатели степени могут быть любыми числами, и которая называется - степенным комплексом.
Вывод - для установления производных единиц измерения пригодны только физические формулы в виде степенных комплексов с постоянным коэффициентом, равным единице.
Определяющее уравнение - степенной комплекс, выбранный для установления производной единицы измерения.
В общем случае производная единица физической величины выражается не только через основные, но и через, ранее установленные - производные единицы других величин.
Общее символическое выражение производной единицы:
{x} = {y1}a1{y2} a2 ... {x1} b1{x2} b2 ... (1.10)
Для простоты определяющего уравнения, как правило, уравнение выбирается так, чтобы оно содержало не более 3- 4-х физических величин, а модули степеней a, b были бы равны единице или двум.
Выражение производной единицы через основные не раскрывает ее физического смысла, но отличается определенной общностью для всех физических величин. Эту форму представления производной физической величины называют размерностью и обозначают - [x].
Так как размер {x} и размерность выражают по-разному, но одну и ту же единицу измерения, то
{x} = [x]. (1.11)
Основная единица обозначается либо символом соответствующей физической величины Y, например, длина L, время T, либо специальным символом, представляющим сокращенно ее название, например, единица длины метр - м, единица времени секунда - с. Первое обозначение преимущественно используется в формулах размерностей [y] = Y, второе - при конкретизации единиц физических величин.
Производная единица обозначается, либо символом представляющем ее название {x} = «название» (единица силы ньютон - Н, работа джоуль - Дж), либо - символом единиц определяющего уравнения (единица скорости м/с, давления Н/м2). В формулах размерностей используется общее обозначение [x].
Если в правой части определяющего уравнения содержаться только размеры основных физических величин, то из
{x} = {y1}a1{y2} a2 ... {x1} b1{x2} b2 ...
при условии {x} = [x] и b1 = b2 = ... = 0
получим формулу размерности:
[x] = [y1]a1[y2] a2 ... (1.12)
Например, для единицы скорости
{v} = {l} {t}-1, [v] = [l] [t]-1
В общем случае формулы размера и размерности различны, например, для единицы силы в СИ
{F} = кг*(м/с)/с, [F] = LMT-2.
Размерность - символическое выражение единицы величины через основные единицы, показывающее соотношение между их размерами без указания этих размеров.
Различают физические величины однородные, одноименные и безразмерные:
Однородные- имеют одинаковую размерность и одинаковый физический смысл. Пример, координаты точек тела и его физический размер.
Одноименные - имеют одинаковую размерность, но разный физический смысл. Пример, работа A = F×s×cos(a), энергия Ек = 1/2m×v2 или Еп=mgh, момент силы M=F×r sin(a) имеют вид [ML2T-2].
Безразмерные - размерность равна единице [x] = [y1]0[y2]0 ... =1, x = x° и не зависят от выбора системы единиц. Пример, относительные изменения любой величины - безразмерная величина Dx/x, отношение дуги окружности к радиусу и т.д.
Все величины, не являющимися безразмерными, называются размерными.
Формула размерности (соотношение между единицами измерения величины и основными единицами) любой физической величины однозначно определяется выбором основных единиц измерения и определяющего уравнения. В то же время, одна и та же формула размерности может соответствовать различным физическим величинам.
Аналогия.
Аналогия- сходство различных объектов по некоторым признакам.
Аналоги - объекты сходные по соответствующим признакам.
Сходственные признаки - признаки, по которым объекты оказываются аналогами.
Сходственные признаки могут иметь качественныйи количественныйхарактер.
В зависимости от этого различают качественную, количественнуюи смешаннуюаналогии.
Основное значение аналогий - перенос сведений с одного объекта на другой (аналог) на основании умозаключений по аналогии.
Умозаключение по аналогии - основано на предположении существования тождественного в различном и выполняется по схеме:
Установлено, что объект O1 обладает свойствами C0, C1, ... , CN, C’1, ..., C’n1.
Установлено, что объект O2 обладает свойствами C1, ... , CN, C’’1, ..., C’’n2.
Вывод: возможно, что объект O2 обладает свойством C0, как объект O1.
Если среди C’’ есть хотя бы одно свойство C’’i несовместное с C0 , то сходство объектов по свойствам C1, ... , CN не имеет никакого значения.
Умозаключение по аналогии имеет гипотетический характер, может привести либо к истинному, либо - ложному выводу.
Пример, аналогия между движением жидкости и процессом распространения тепла привела к неправильному выводу о существовании теплорода.
Суждение, полученное по аналогии, нуждается в специальной проверке. Вероятность правильности этого суждения тем больше, чем сильнее связь между свойствами C, чем слабее связь между C и C’ и между C и C’’, чем больше N и чем меньше n1 n2.
Умозаключение по аналогии имеет доказательный характер, если общие свойства объектов C1, ... , CN обуславливают свойство C0.
Умозаключение по аналогии - является основой аналогичного моделирования, пример, замещение организма человека организмом животного с целью исследования действия новых лекарств, что неоценимо важно для развития медицины.
Общенаучное значение аналогий - прежде всего для придания наглядности, аналогия электрического тока с движением жидкости, для формирования понятий и для иллюстрации. Примеры понятий, введенных по аналогии, - теплоемкость, запоминающее устройство, электродвижущая сила. Пример иллюстрации по аналогии - иллюстрацией понятия устойчивости служит система - шарик на вогнутой поверхности в поле тяготения.
Кроме того, аналогия может служить и как активизатор мышления, и как источник идей.
Пример: соотношения 11 + 21 = 31 , 32 + 42 = 52 по аналогии привели математика П. Ферма к уравнению xn + yn = zn с тремя неизвестными и к формулировке «великой теоремы» теории чисел, согласно которой это уравнение при любом целом n>2 не имеет целых положительных решений. Справедливость теоремы Ферма доказана для всех n £ 100, но в общем виде она остается недоказанной.
Подробный пример: известно, что если все корни алгебраического уравнения a0 + a1x + a2x2 + ... + anxn = 0, a > 0, вещественные отрицательные и разные, | x1 | < | x2 | < ... < | xn |, то | xi | = ai-1/ai. Если модуль каждого корня значительно превышает модуль предыдущего, т.е. | xi-1 | << | xi |, то
ao/a1<a1/a2<a2/a3< ... <an-1/an. (1.13)
Известно, что если непрерывная линейная стационарная САУ с характеристическим уравнением
A0 + A1p + A2p2 + ... +Anpn = 0, A > 0 (1.14)
устойчива, то алгебраические уравнения
A0 + A2y + A4y2 + ... = 0
A1 + A3Y + A5Y2 + ... = 0
имеют только вещественные отрицательные чередующиеся корни |y1| < |Y1| < |y2| < |Y2| < ... Если модуль каждого из этих корней значительно превышает модуль предыдущего, т.е. | yi-1 | << | Yi | << | yi+1 |, то аналогично (1.13)
A0/A2 < A1/A3 < A2/A4 < ... < An-2/An . (1.15)
Эта аналогия приводит к идее использовать ряд отношений четных и нечетных коэффициентов (1.15) для анализа устойчивости непрерывных линейных стационарных систем и к грубому критерию устойчивости. Этот критерий требует составления ряда (1.15) и нахождения значений
ai = Ai / Ai+2, ki = ai / ai-1 = (Ai / Ai+2) / (Ai-1 / Ai+1) = AiAi+1 / Ai-1Ai+2,
а также определяет достаточные условия устойчивости (все ki ³ 2.15) и неустойчивости (хотя бы одно ki £ 1). Простота критерия позволяет обойтись в некоторых случаях без всяких расчетов и констатировать устойчивость или неустойчивость, основываясь на простом обозрении ряда (1.15). Условие неустойчивости ki £ 1 или соответствующее ему Ai-1Ai+2 £ AiAi+1 может быть установлено простым обозрением уравнения (1.14).
«Стандартным» методом генерации идей на основании аналогии является обобщение. Например, переход от биквадратных уравнений к бикубическим и биалгебраическим, от комплексных чисел к гиперкомплексным, от обычного преобразования Лапласа к многомерному и двустороннему.
Существенное значение аналогии заключается в возможности использовать ее для строгих выводов и доказательств.
Аналогия позволяет перейти к понятию подобия. Вид количественной аналогии - аналогия математическая - сходство объектов по их математическому описанию.
Сходственные функции - функции, различающиеся только аргументами и ненулевыми постоянными. Пример, z = x cos y и u = 2v cos 3w или r = 4s cos (5t + 6) и q = 7p cos (8l + 9) являются сходственными.
Сходственные переменные - переменные величины, входящие под знаки сходственных функций совершенно одинаковым образом.
Сходственные постоянные - аналогично сходственным переменным. Сходственные функции 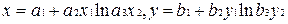 содержит сходственные переменные
содержит сходственные переменные 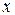 и
и 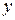 ,
, 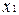 и
и 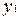 ,
, 
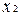 и
и 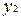 , сходственные постоянные
, сходственные постоянные 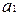 и
и 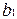 ,
, 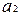 и
и 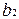 ,
, 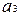 и
и 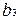 .
.
Сходственные уравнения - получают приравниванием нулю или друг другу сходственных функций.
Наиболее полная математическая аналогия имеет место, если объекты описываются сходственными функциями и уравнениями.
Дата добавления: 2015-11-10; просмотров: 1103;
