Способы создания моделей

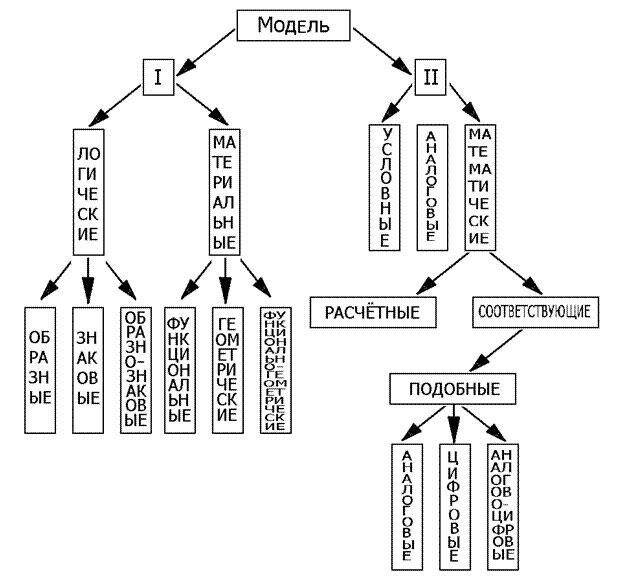Классификация моделей

В основу классификации положены наиболее важные признаки моделей:

1. Закон функционирования и характерные особенности выражения свойств и отношений оригинала;

2. Основания для преобразования свойств и отношений модели в свойства и отношения оригинала.

По первому признаку модели разделяют на логические - образные, знаковые, образно - знаковые и материальные - функциональные, геометрические, функционально - геометрические. Логическиемодели функционируют по законам логики в сознании человека. Материальные - по объективным законам природы.

Логические модели:

* Образные (иконические) модели - выражают свойства оригинала с помощью наглядных чувственных образов, имеющих прообразы среди элементов оригинала или объектов материального мира. Пример, частицы газа в виде упругих шаров (кинетическая теория газа).

* Знаковые (символические) модели - выражают свойства оригинала с помощью условных знаков и символов. Пример, математические выражения и уравнения, физические и химические формулы и т.п.

* Образно - знаковые модели - обладают признаками образных и знаковых моделей. Пример: схемы, графики, чертежи, графы, структурные формулы, иероглифы и т.п.

Материальные модели:

* Функциональные модели - отражают основные функциональные свойства оригинала. Пример, моделью маятника, совершающего колебательное движение, может служить RLC-цепочка.

* Геометрические модели - отражают пространственные свойства оригинала. Пример, глобус.

* Функционально - геометрические модели - отражают одновременно функциональные и пространственные свойства оригинала. Пример, макет самолета в аэродинамической трубе.

В зависимости от физической однородности и разнородности с оригиналом функциональныеи функционально - геометрические модели разделяются на физические и формальные. Пример, работу электрического генератора необходимо исследовать на активно - емкостной потребитель, подключение к которому по каким-либо причинам невозможно, потребитель можно заместить на последовательную цепь из резистора и конденсатора. В этом случае эта цепь является физической моделью потребителя. Если оригинал - маятник, то электрический колебательный контур является его формальной моделью.

По второму признаку модели делятся на условные, аналогичные и математические.

* Условные модели - выражают свойства и отношения оригинала на основании принятого условия (соглашения). Сходство с оригиналом у таких моделей может совершенно отсутствовать. К ним относятся все знаковые и образно - знаковые модели.

* Аналогичные модели - обладают сходством с оригиналом, достаточным для перехода к оригиналу на основании умозаключения по аналогии, т.е. на основании логического вывода, что, оригинал, возможно, обладает некоторым признаком, имеющимся у модели, так как другие признаки оригинала сходны с признаками модели. Пример, все виды макетов кораблей, самолетов и т.д.

* Математические модели – модели, в которых основные функциональные свойства объекта заменяются математическими выражениями. Они обеспечивают переход к оригиналу, фиксацию и исследование его свойств и отношений с помощью математических методов.

Математические модели делятся на расчетные и соответствующие:

Расчетные - выражают свойства и отношения оригинала с помощью математических представлений - формул, уравнений, графиков, таблиц, операторов, алгоритмов и т.д. Пример, объект Z=X*Y – модель выходная координата.

Соответствующие – модели, в которых переменные величины модели связаны с соответствующими переменными величинами оригинала определенными математическими зависимостями. Пример, если две функции Z=XY и z=x+y, а также их независимые переменные связаны соотношениями x= lgX, y =lgY, z = lgZ, то каждый из таких объектов может служить соответственной моделью другого.

Математические модели имеют признаки условных моделей и могут обладать признаками аналогичных.

Среди соответствующих моделей можно выделить важнейший класс – подобные модели, которые как класс формируются на основе теории подобия.

Подобные модели - переменные величины, в которых пропорциональны соответствующим переменным оригинала. Подобные модели также могут быть логическими и материальными. Подобные материальные модели подразделяются на аналоговые (непрерывные), цифровые (дискретные) и аналого-цифровые (комбинированные и гибридные), это зависит от того, какие величины связывает их математическое описание - непрерывные, дискретные или те и другие вместе.

Аналоговые -модели, в которых основные функциональные свойства объекта заменяются подобными функциональными свойствами модели любой природы.

Цифровые - модели, в которых основные функциональные свойства объекта моделируются дискретно.

Аналогово-дискретные –модели, которые сочетают в себе аналоговую и дискретную части (одни свойства объекта выражаются аналоговыми, другие – дискретными моделями).

Подобие оригинала и его материальной модели позволяет использовать последнюю в качестве вычислительного устройства для решения уравнений, описывающих оригинал.

Согласно общей теории моделирования, все вычислительные устройства являются материальными подобными моделями соответствующих материальных или логических оригиналов.

В зависимости от характера математического описания эти устройства могут быть аналоговыми, цифровыми и аналого-цифровыми.

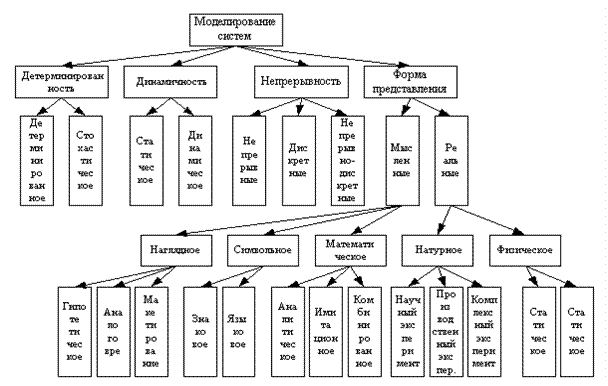Классификация методов моделирования

Моделирование систем включает в себя модели объекта с одной стороны и способы отражения их функционирования с другой.

По характеру изучаемых процессов моделирование может классифицироваться по следующим признакам: детерминированность, динамичность, непрерывность и форма-представление.

С точки зрения детерминированности различают: детерминированное и стохастическоемоделирование. При детерминированном моделировании используются детерминированные методы без учета случайных воздействий внешней среды. Стохастическое моделирование отображает вероятностные и случайные процессы в объекте. При этом используется математический аппарат статистики и вероятностных процессов.

С точки зрения динамичности разделяют статическое и динамичное моделирование. Динамичное моделирование процессы, происходящие в объекте, рассматривает во времени. Статическое моделирование изучает особые статические режимы, когда процессы, происходящие в объекте, не зависят от времени.

По признаку непрерывности различают: непрерывное, дискретное и непрерывно-дискретное моделирование. Непрерывное моделирование рассматривает процессы, происходящие в объекте, непрерывно в течение всего времени исследования. Математическим аппаратом данного типа моделирования являются дифференциальные уравнения. Дискретное моделирование изучает процессы в определенные моменты времени, математический аппарат – разностные уравнения. Непрерывно-дискретное моделирование сочетает в себе свойства непрерывного и дискретного моделирования.

По формам представления моделирование может быть мысленное (логическое) и реальное (материальное).

Мысленное моделированиеприменяется при исследовании систем, которые по каким-либо причинам не может быть реализовано физически. Мысленное моделирование в свою очередь разбивается на три крупных класса:

Наглядное моделирование - это создание наглядных моделей на базе представлений человека об объекте.

Наглядное моделирование подразделяется на гипнотическое, аналоговое и макетирование.

· Гипнотическое моделирование – это исследование модели в виде черного ящика, при этом структура и функциональные особенности объекта представляются гипотезой. После выдвижения гипотезы она либо принимается, либо нет.

· Аналоговое моделирование применяется в том случае, когда любое функциональное свойство объекта заменяется аналоговым.

· Макетирование применяется в случае, если невозможна физическая реализация объекта. Модель представляет собой полную аналогию с исследуемым объектом, но в другом масштабе.

Символьное моделирование – замена реального объекта неким набором символов (любому объекту ставится в соответствие символ). Выделяют языковое и знаковое моделирование.

· При знаковом моделировании вводятся символьные обозначения определенных понятий, однородные понятия объединяются в отдельные множества. Все знаковое моделирование сводится к теории множеств и операциям между ними.

· При языковом моделировании объекту и процессам, происходящим в нем, ставится в соответствие тезаурус – язык, лишенный двусмысленности, т.е. его символика похожа на символику нашего языка, но все однозначно.

Математическое моделирование подразделяется на аналитическое, имитационноеи комбинированное.

· Аналитическое моделирование – определенному объекту ставится в соответствие система уравнений и методы ее решения (высшая математика). Применяется при исследовании относительно несложных систем, к которым относится САУ.

· Имитационное моделирование – отдельные свойства объекта имитируются конкретными математическими способами (нет конкретной модели), используется для исследования сложных систем. Как правило, применяется к стохастическим моделям и системам массового обслуживания. Для имитационного моделирования применяется пакет GPSS.

· Комбинированное моделирование – это моделирование, в котором используются элементы аналитического и имитационного.

Реальное моделированиеможет быть натурным и физическим.

Натурное моделирование – это проведение исследований с реальными объектами с последующей обработкой результатов эксперимента.

В нем выделяют:

· производственный эксперимент – воспроизведение на натурном объекте основных режимов производственного процесса для дальнейшего исследования.

· научный эксперимент – воспроизведение на натурном объекте качественно новых режимов, увеличение технических границ.

· комплексный эксперимент – сочетает в себе элементы научного и производственного эксперимента

При постановке научного эксперимента реальный объект используется в качественно новых условиях функционирования или при воздействии новых факторов внешней среды с последующей обработкой результатов.

Физическое моделирование:

· в реальном масштабе времени – осуществляют постановку эксперимента в одинаковых масштабах времени как для объекта, так и для модели.

· в нереальном масштабе времени – при постановке эксперимента масштабы времени для модели и объекта различаются на некоторую величину.

Глава 2