Основные положения теории размерности
Измерить некоторую величину Р – это значит сопоставить ее с другой величиной Q той же физической природы и определить, во сколько раз Р больше или меньше Q. При этом величина Q называется единицей измерения.
Системой единиц измерения называют совокупность установленных единиц измерения, которые подразделяются на основные и производные.
Пример: СИ включает в себя следующие единицы:
Таблица 3
| Обозначение | Размерность | Ед. измерения | |
| 1. Длина | l | L | м |
| 2. Масса | m | M | кг |
| 3. Время | t | T | с |
| 4. Сила тока | i | I | А |
| 5. Термодинамическая температура | T | Q | К |
| 6. Количество вещества | m | N | моль |
| 7. Сила света | J | J | канделла |
Производные единицы образуются из основных единиц на основе физических законов, устанавливающих взаимосвязь между величинами исходного объекта и величинами, единицы измерения которого приняты в качестве основных.
Формула размерности или размерность – это соотношение между единицами измерения этой величины и основными единицами. Различают однородные, безразмерные, одноименные физические величины.
Однородные величины – величины, имеющие одинаковую размерность и одинаковый физический смысл.
Одноименные величины – величины, имеющие одинаковую размерность, но различный физический смысл. Пример: индуктивность и взаимоиндуктивность, диффузии и вязкость.
Безразмерными величинами называют величины, размерность которых равна 1, эти величины не зависят от единиц измерения.
Группой независимых параметров называют совокупность параметров, размерность каждого из которых не может быть выражена через размерность параметров этой группы.
Математическое условие независимости параметров – для группы параметров 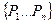 признаком независимости является наличие хотя бы одного отличного от нуля определителя порядка n. Исходная матрица формируется из показателей степеней при основных единицах измерения данных параметров.
признаком независимости является наличие хотя бы одного отличного от нуля определителя порядка n. Исходная матрица формируется из показателей степеней при основных единицах измерения данных параметров.
Пример: 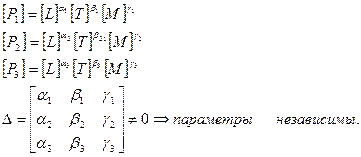
Критерии подобия
Степенным комплексомназывается функция следующего вида y = x1a × x2b × …× xnw.
Основные свойства степенных комплексов:
1. Число простых степенных комплексов, образованных из некоторых величин, не превышает количество этих величин. Составными называются комплексы, получаемые на основе простых.
Пример: {x1 x2 x3}
 k1 = x1 x2
k1 = x1 x2
k2 = x1 x22 x3 ki = f(k1 …ki-1)
k3 = x1 x23 x3
k2 = x13 x24 x3
k1 = x1 x2 Þ x1 = k1 /x2
k2 = x1 x22 x3 Þ x2 x3 = k2/ k1
k3 = x1 x23 x3 Þ k3 = k12 ×k2/ k1 = k2 × k1
k4 = x13 x24 x3 Þ k4 = k12 ×k2
Таким образом
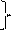 k1 = x1 x2 простые критерии
k1 = x1 x2 простые критерии
k2 = x1 x22 x3
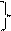 k3 = k2 × k1 составные критерии
k3 = k2 × k1 составные критерии
k4 = k12 ×k2
2. Любая функция может быть представлена в виде функции стенного комплекса
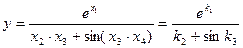
3. Любую безразмерную функцию размерных величин можно представить в виде функции безразмерных степенных комплексов, образованных из этих величин.

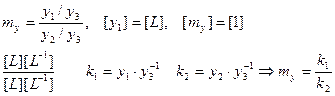
4. Любую размерную функцию размерных величин можно представить в виде произведения размерного степенного комплекса, составленного из этих величин и безразмерной функции этих же величин.
y = F(x1x2…xn)
[y] ¹ [1]
[xi] = [1] i = 1…n
[y] = [k]
F(x1x2…xn) = k× Ф(x1x2…xn), где [Ф] = 1
Дата добавления: 2015-11-10; просмотров: 2004;
