Подобие физических процессов (объектов)
Любой конкретный физический процесс j0 характеризуется функциональной зависимостью F между параметрами P1, P2, ..., Pj, …, Pn. Эту функциональную зависимость Д0 = F(P1, P2, ..., Pj…, Pn) можно графически отобразить в соответствующем n - мерном координатном пространстве x1, ...,.xj, ..., xn. В этом координатном пространстве каждый параметр соотнесен с определенной координатной осью.
Аналогично в том же координатном пространстве может быть отображен другой процесс Ф0 = F(R1, ..., Rj, …, Rn), который характеризуется сходными с Д0 параметрами. Два физических процесса будут подобны, если сходственные параметры пропорциональны, т.е. если 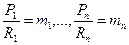 , а функциональные зависимости идентичны. В этом случае Д0 и Ф0 подобны.
, а функциональные зависимости идентичны. В этом случае Д0 и Ф0 подобны.
Не все масштабные коэффициенты m1, ..., mj, ..., mn могут принимать независимые значения, вследствие того, что зависимы параметры, которые характеризуют процесс. Это делает возможным введение обобщенных характеристик подобных процессов - критериев подобия. Критерии подобия - это функции групп зависимых и независимых параметров. Если масштабные коэффициенты, в общем случае численно различны, то критерии подобия принимают одинаковые значения в сходственных точках обобщенного пространства параметров x1, ...,.xj, ..., xn.
Пропорциональность параметров - частный случай подобия физических процессов. Понятие сходственных точек и величин значительно сложнее в теории подобия физических явлений, нежели в геометрии.
Сходственные точки пространства, времени и параметров процесса - это такие величины, при которых их значениям в одной системе так или иначе соответствуют значения в другой системе.
Сходственные функции –отличаются друг от друга аргументами и постоянными
x1 = a sin(x2t+c) и y1 = b sin(y2t+d).
Сходственные переменные – это переменные величины, которые входят в сходственные функции: x1и y1 , x2 и y2 .
Сходственные уравнения получаются из сходственных функций путем преобразования к однородному уравнению и приравниванию между собой.
Подобие- это взаимооднозначное соответствие между объектами (процессами), при котором функции или правила перехода от параметров, характеризующих один из объектов, к параметрам, в том же смысле характеризующих другой объект, известны, а математические описания допускают их преобразования к тождественному виду.
Виды подобия.
Рис.10 Виды подобия
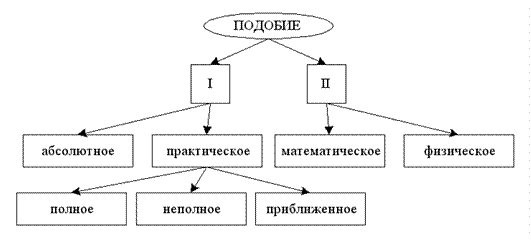 |
Виды подобия различаются по двум основным признакам:
I. степень соответствия параметров оригинала и модели (абсолютное и неабсолютное или практическое подобие, которое может быть полным, неполным и приближенным);
II. адекватность физической природы подобных явлений (математическое подобие и физическое подобие, которое может быть механическим, тепловым, электрическим и т.п.)
Сходственные величины (точки) – это величины, которые, так или иначе, соответствуют величинам другого объекта. Сходственные функции отличаются друг от друга аргументом и постоянными.

Сходственные переменные – переменные величины, которые входят в сходственные функции.
x2 ~ y2
Сходственные уравнения – получаются из сходственных функций путем преобразования к однородному (равному нулю) уравнению при дальнейшем приравнивании между собой.
Два объекта абсолютно подобныдруг другу, если в сходственные моменты времени в сходственных точках пространства параметры одного объекта Pi находятся в некотором соответствии с параметрами другого объекта Ri .
Pi/ Ri = mi Þ а) mi = const ® геометрическое подобие
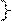 б) mi ¹ const ® аффинное или физическое подобие
б) mi ¹ const ® аффинное или физическое подобие
mi = f(bi)
Абсолютное подобие в значительной мере носит абстрактный характер. Реализуется только в геометрических построениях и в отдельных видах математического подобия.
Практическое подобие отличается от абсолютного тем, что рассматриваются не все процессы в сравниваемых объектах. В зависимости от того какие процессы рассматриваются. Различают полное, неполноеи приближенное подобие.
· Полное практическое (слово «практическое» далее опускается) подобие - подобие протекания во времени и в пространстве только тех процессов, которые существенны для данного исследования. (Если, например, электромеханические явления в синхронных генераторах полностью подобны, то все процессы изменения во времени токов, напряжений, вращающих моментов и изменение во времени и в пространстве распределения магнитных и электрических полей отличаются только масштабами. При этом тепловые явления могут быть неподобными, так как они не влияют на подобие исследуемых электромеханических процессов).
· Неполноеподобие - подобие протекания процессов только во времени или только в пространстве. (Например, есть подобие электромеханических процессов во времени, но нет подобия распространения полей).
· Приближенноеподобие - характеризуется наличием допущений, приводящих к допустимым искажениям одного из процессов. Приближенное подобие бывает также полным и неполным. (Например, подобие генераторов, устанавливаемое по упрощенным уравнениям, которые не учитывают апериодическую составляющую тока статора и периодическую составляющую тока ротора.)
По II признаку различают математическое и физическоеподобие.
· Физическое подобие - когда одинакова физическая природа подобных явлений. Бывает полное, неполное и приближенное. Например: механически подобным процессам ставятся в соответствие - механические, электрическим - электрические, тепловым - тепловые и т.д., т. е. модель функционирует на тех же физических законах, что и сам объект.
· Математическоеподобие - когда сходственные параметры сравниваемых процессов различной физической природы соответствуют друг другу. Бывает полное, неполное и приближенное.
Пример математического подобия:
1) Уравнение переходного процесса в электрической цепи (последовательное соединение резистора R, индуктивности L и конденсатора C), включенной на переменное напряжение u, изменяющееся во времени t по синусоидальному закону с угловой скоростью w. Где q заряд на пластинах конденсатора С.
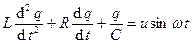
2) Уравнение процесса вынужденных механических колебаний в вязкой среде груза массы M на пружине жесткостью с, под действием возмущающей силы F = sin wt и пропорциональной скорости движения груза v силы сопротивления вязкой среды F = - kv, где l - расстояние, на которое перемещается груз, а k – коэффициент вязкости среды, в которой перемещается маятник.
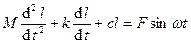
Сходственными параметрами в данном случае будут M и L, k и R, c и C, u и F, а электрический колебательный контур может служить аналоговой моделью объекта - оригинала (колеблющегося на пружине груза), наблюдаемый процесс в колебательном контуре будет одновременно решением дифференциального уравнения, описывающего движение груза.
Таким образом, теория подобия позволяет установить наличие подобия между двумя процессами или разработать способы получения этого подобия.
Основными составляющими теории подобия являются:
1. Теория размерности;
2. 3 теоремы подобия.
Теория размерности
Дата добавления: 2015-11-10; просмотров: 2670;
