Содержащими только однородные функции

Рассматриваются необходимые для определения критериев подобия преобразования, одновременно пример преобразования уравнения переходного процесса i(t) в последовательной цепи из активного сопротивления R и индуктивности L, которая включается на постоянное напряжение u.

Имеются уравнения двух подобных процессов j₀ и F₀, являющихся функциями параметров P₁, P₂, ..., P_j, ..., P_n и R₁, R₂, ..., R_j, ...,R_n соответственно, то есть в общем случае:

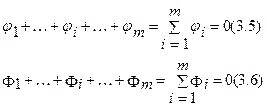или

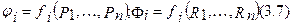
члены уравнений для j ₀ и F₀; i = 1, 2, ..., m.

Для рассматриваемого примера уравнения двух переходных процессов - это два дифференциальных уравнения:

i₁R₁ + L₁di₁/dt₁ - u₁ = j ₁ + j ₂ + j ₃ = (3.5а)

i₂R₂ + L₂di₂/dt₂ - u₂ = F ₁ + F ₂ + F ₃ = 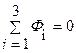(3.6а)

где

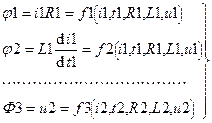(3.7а)

Сопоставляемые процессы j₀ и F₀ подобны, следовательно, между их сходственными параметрами должны существовать соотношения пропорциональности вида:

P₁ = m₁R₁, ..., P_j = m_jR_j, ..., P_n = m_nR_n (3.8)

или

R₁ = m_RR₂; L₁ = m_LL₂; u₁ = m_uu₂; (3.8а)

i₁ = m_ii₂; t₁ = m_tt₂

где m₁, ..., m_j, ..., m_n или m_R, m_L, m_i, и m_t - масштабные коэффициенты.

В соответствии с первой теоремой подобия для подобных процессов j₀ и F₀, все члены уравнений которых однородные функции, должны существовать одинаковые критерии подобия. Их отыскивают приведением уравнения к безразмерному виду.

К безразмерному виду уравнения приводятся делением их на какой либо, например на m-й, член (j_m и F_m):

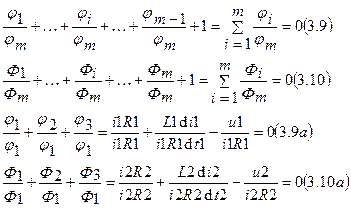
Вследствие однородности (3.5) и (3.6) в выражениях для j_i и F_i существуют некоторые общие множители, которые можно вынести за знак функции. Общий множитель для i-го члена j_i исходного уравнения (3.5) - некоторая комбинация масштабных коэффициентов m₁, ..., m_j, ..., m_n, т.е. в соответствии с (3.7) и (3.8):

j_i = f_i (P₁, ..., P_j, ..., P_n) = f_i (m₁R₁, ..., m_jR_j, , m_nR_n) = M_if_i (R₁, ..., R_j, ..., R_n) = M_iF_i (3.11)

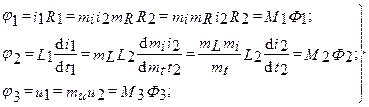(3.11a)

Подстановка (3.11) в (3.9) дает

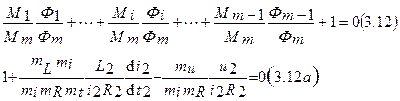
Поскольку уравнение (3.12) представляет собой сумму однородных функций, должен существовать общий для всех его членов множитель M_m:

M₁ = ... =M_i = ... = M_m-1 = M_m (3.13)

или

M₁/M_m = ... =M_i/M_m = ... = M_m-1/M_m = M_m/M_m =1 (3.14)

Это означает, что

1 = m_L/(m_Rm_t) = m_u/(m_im_R) (3.14a)

Физический смысл результата: как исходное уравнение (3.5а), так и преобразованное (3.12а) описывают процесс j₀, т.е. переходный процесс i₁(t₁). Подобие процессов j₀ и F₀ означает, что они должны описываться одинаковыми уравнениями, так как имеют одинаковый качественный характер и различаются только масштабами.

Вывод: формула (3.12а) будет описывать F₀ - переходный процесс i₂(t₂) - только в том случае, если будут равны единице комбинации масштабных коэффициентов при втором и третьем членах (3.12а).

Тождественность (3.12) и (3.9) означает, что между соответственными членами (3.5) и (3.6) существуют отношения:

j₁/j_m = F₁/F_m, ..., j_i/j_m = F_i/F_m, ..., j_m-1/j_m = F_m-1/F_m (3.15)

Обобщая (3.15) на произвольное число s подобных процессов, уравнения которых содержат только однородные функции, можно записать:

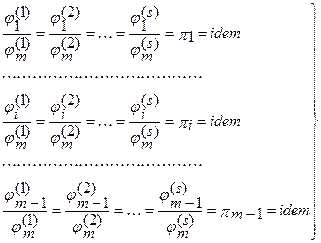(3.16)

где (1), (2), (i), ..., (s) номера сопоставляемых процессов, idem - означает «соответственно одинаково для всех рассматриваемых процессов».

Для рассматриваемого процесса:

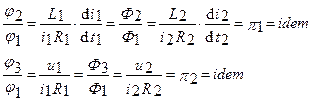
В общем случае соотношения пропорциональности вида (3.8) справедливы на любых (и малых, и больших) интервалах изменения сопоставляемых функций. Поэтому символы дифференцирования и интегрирования при рассмотрении условий пропорциональности можно опустить, так как они не имеют размерности и не влияют на условия пропорциональности, заменив соответствующие члены уравнений j_j на их аналоги j_j^*, которые называются интегральными, т.е. заменить dⁿx/dyⁿ на x/yⁿ и òxdy на xy.

Для рассмотренного примера:

j₂^* = L₁(i₁/t₁); j₁^* = i₁R₁; p₁ = j₂^*/j₁^* = L₁i₁/i₁R₁t₁ = L₁/R₁t₁

где j₂^* и j₁^* аналоги j₂ и j₁.

Опуская индексы номеров процесса (1), (2), ..., (s), можно с учетом (3.14) записать:

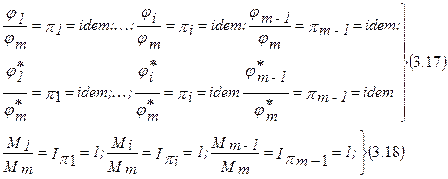
где j₁, ..., j_m - члены исходного уравнения (3.5); j₁^*, ..., j_m^* - интегральные аналоги j₁, ..., j_m; M₁, ..., M_m - комбинация (произведения или отношения) масштабных коэффициентов.

Применительно к примеру:

L/tR = p₁ = idem; u/iR = p₂ = idem (3.17a)

m_L/m_Rm_t = Ip₁ = 1; m_u/m_im_R = Ip₁ = 1 (3.18a)

Выражения (3.17) для критериев подобия, иногда называемые инвариантами подобия, имеют вид безразмерных степенных комплексов:

p_i = P₁^z1 ... P_j^zj ... P_n^xn = idem (3.19)

Для рассматриваемого примера:

p₁ = L/Rt = L¹R^-1t^-1 = L¹R^-1t^-1i⁰u⁰ = idem

p₂ = u/iR = u¹ i^-1R^-1 = L⁰R^-1t⁰i^-1u¹ = idem (3.19a)

Число K_j критериев подобия, найденных приведением к безразмерному виду, на единицу меньшечисла членов m, входящих в уравнение, K_j = m-1.

Точки координатного пространства, в которых критерии подобия численно равны j⁽¹⁾ и j⁽²⁾, или j⁽¹⁾ и j⁽³⁾ и т.п. называются сходственными точками: только в этих точках пропорциональны все сходственные параметры сопоставляемых подобных процессов. При этом масштабные коэффициенты сходственных параметров подобных процессов подчиняются условиям (3.18); не существуют подобные процессы с иными соотношениями сходственных параметров. Выражения вида (3.18), при которых соблюдаются соотношения (3.17), называются, иногда, индикаторами подобия.