Определение критериев подобия процессов, описываемых уравнениями, содержащими неоднородные функции

Если часть членов уравнения, описывающего рассматриваемый процесс, неоднородные функции, то масштабные коэффициенты нельзя вынести за знак функции и, следовательно, преобразования приведенные выше - невозможны. В этих случаях у подобных процессов должны быть равны аргументы неоднородных функций.

Уравнения 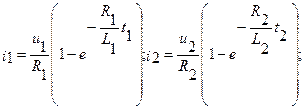будут тождественны, если

exp [(-R₁/L₁)t₁] = exp [(-R₂/L₂)t₂],

т.е. если

.

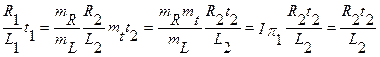Т.е. необходимо потребовать равенства показателей степеней экспоненциальных (неоднородных) функций и принять этот показатель степени в качестве критерия подобия, т.е.:

p₁^’ = R₁t₁/L₁ = R₁t₁/L₁.

После преобразования уравнений для i₁(t) и i₂(t) к безразмерному виду критериями подобия сопоставляемых процессов будут:

,

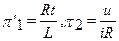или, если принять p₁ = (p₁^’)^-1, то как и ранее

,

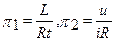что и следовало ожидать, так как рассматриваются различные формы математического описания одного и того же физического процесса.

Аналогично для уравнений содержащих тригонометрические функции

если 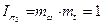, т.е. необходимо ввести дополнительный критерий подобия

p_доп. = wt.

Преобразование критериев подобия

Возможность преобразования критериев подобия - их важное практическое свойство.

Определение: критерии подобия процесса, представленные в какой-либо форме записи, могут быть преобразованы в критерии подобия иной формы записи посредством перемножения или деления их, возведения в степень или умножения на любой постоянный коэффициент k.

Если, например, совокупность критериев подобия p₁, p₂, ...,p_k, ..., p_k+j, ..., p_m, полностью описывает некоторый физический процесс, то и совокупность критериев подобия p₁^’ = kp₁, p₂^’ = p₂^-1, ..., p_k^’ = p_k p_k+j, p^’_k+j = p_k+j/p_m, ..., p^’_m = (p_m)^k также будет полностью характеризовать этот процесс, т.к. при

p₁ = idem, ..., p₂ = idem, ..., p_k = idem, ..., p_k+j = idem, ..., p_m = idem.

p₁^’ = kp₁ = idem, p₂^’ = 1/p₂ = p₂^-1 = idem, ..., p_k^’ = p_k p_k+j = idem, ..., p^’_k+j = p_k+j/p_m = idem, ..., p^’_m = (p_m)^k = idem.