Методика определения критериев подобия на основе анализа размерностей

Анализ размерностей параметров, участвующих в процессе, позволяет получить выражения для критериев подобия в наиболее общем случае, когда математическое описание этого процесса неизвестно.

Исходные положения:

1. Полное физическое уравнение f(P₁, P₂, P₃, P₄, ..., P_i, ..., P_m) =0 учитывает все связи между входящими в него величинами P₁, ..., P_m и справедливо при изменении системы единиц измерения этих величин.

Неполное уравнение - f(P₁, P₂, P₃, K₁, ..., K_j, ..., K_n) = 0 - отражает только некоторые частные зависимости между переменными (P₁, P₂, P₃), справедливые в том случае, если переменные (P₄, ..., P_m), определенные при конкретных условиях, далее полагаются постоянными применительно к некоторым частным случаям (т.е. коэффициентами (K₁, ..., K_j, ..., K_n; K_j = const, j = 1, ..., n). Неполное уравнение становится полным, если рассматривать коэффициенты K_j как величины, имеющие размерность и изменяющиеся при изменении системы единиц измерения, т.е. раскрыть функциональные связи вида

K_j = f_j( P₄, ..., P_i, ..., P_m), j = 1, ..., n.

2. Единица измерения физической величины.

3. Система единиц измерения.

4. Основные единицы измерения.

5. Производные единицы измерения.

6. Формула размерности.

7. Однородные, одноименные и безразмерные физические величины.

8. Параметры с независимыми размерностями (независимые параметры) и параметры с зависимыми размерностями (зависимые параметры).

Группой независимых параметров называется такая группа параметров, в которой размерность ни одного из не может быть образована из размерностей других параметров, принадлежащих той же группе. Пример: две группы параметров (l, m, v) и (l, t, v), в первой группе параметры независимы, во второй - зависимы, т.к. v = l/t. Если параметры зависимы, то нельзя все характеристики выбирать произвольно. Пример: произвольно выбрав величины для измерения тока и напряжения, нельзя произвольно выбирать величины, измеряющие сопротивления и мощность.

9. Признаком независимости параметров P₁, P₂, P₃, ..., P_k является существование хотя бы одного определителя порядка k отличного от нуля, который образуется из элементов матрицы, составленной из показателей степеней при основных единицах измерения в формулах размерностей этих параметров. Пример:

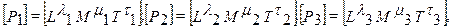
для независимости группы параметров P₁, P₂ и P₃ необходимо неравенство нулю определителя

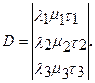
10. Для физического процесса, полностью характеризуемого m размерными параметрами P₁, ..., P_k, P_k+1, ..., P_s, ..., P_m, среди которых k параметров P₁, ..., P_k являются независимыми, существует m - k критериев подобия p₁, ..., p_m-k. Число k равно рангу матрицы, образованной показателями степеней при основных единицах измерения.

Методика определения критериев подобия путем анализа размерностей участвующих в процессе факторов сопровождается примером определения критериев подобия переходного процесса i(t) для последовательной цепи с активным сопротивлением R, индуктивностью L, емкостью C, включенной на напряжение u, меняющееся во времени по синусоидальному закону с угловой скорость w.