Этапы определения критериев подобия

I. Выявление параметров P₁, ..., P_i, ..., P_m, характеризующих рассматриваемый процесс.

Соотношение, отражающее существенные связи между параметрами процесса и элементов системы, в которой процесс протекает, представляется полной функциональной зависимостью вида

f(P₁, ..., P_i, ..., P_m)

или для примера (m = 7)

f( i, t, R, L, C, u, w).

II. Составление полной матрицы размерностей ||A|| для параметров P₁, ..., P_m. Для составления матрицы размерности всех параметров P₁, ..., P_m записываются в основных единицах выбранной системы измерения [ a, b, ..., q ], для примера - система СИ - [ L, M, T, I ].:

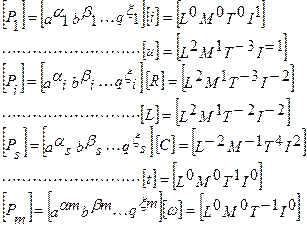
Количество строк полной матрицы размерностей ||A|| соответствует общему числу параметров m, а количество столбцов - числу основных единиц измерения q, строки матрицы образуются показателями степеней при основных единицах измерения параметров.

Полная матрица ||A|| размером m ´ q, в примере 7 ´ 4, т.к. m = 7, q = 4, имеет вид

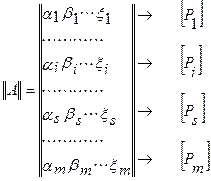или

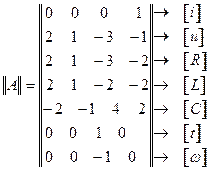
символ ® соответствие.

III. Определение числа независимых параметров и числа критериев подобия. Число k независимых параметров равно рангу k полной матрицы размерностей ||A||, а число критериев подобия K_p - разности между общим числом параметров m и числом независимых параметров k. Ранг матрицы - наибольший порядок отличного от нуля определителя, который составлен из элементов строк данной матрицы с сохранением порядка их следования.

Число k независимых параметров не может превышать числа q основных единиц измерения, следовательно, ранг матрицы всегда не больше q (k £ q). Общее число определителей N_q порядка q равно сочетанию из m по q (в примере m = 7, q = 4)

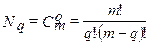или, для примера N_q = 35. Все определители 4-го порядка равны нулю. Далее анализируются определители порядка q - 1, и т.д. В примере не равен нулю определитель 3-го порядка, у частичной матрицы составленной из второй, третьей и пятой строк полной матрицы, два из четырех возможных определителей не равны нулю, следовательно, ранг полной матрицы ||A|| равен трем 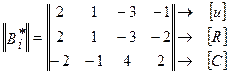. Поэтому число независимых параметров k = 3, число критериев подобия K_p = m - k = 7 - 3 = 4.

В общем случае, признаком зависимости является пропорциональность соответствующих строк матрицы либо возможность представления какой-либо из ее строк в виде линейной комбинации других строк.

IV. Определение конкретного состава группы независимых параметров P₁, ..., P_k и числа форм записи критериев подобия F_p.

В состав группы из k независимых параметров входят такие параметры, для которых существует хотя бы один определитель не равный нулю порядка k, составленный из элементов частичной матрицы размерностей размером k ´ q. В примере такую группу образуют параметры u, R, C, которым соответствует частичная матрица размерностей ||B_i^*||. Общее число возможных форм записи критериев подобия F_p равно: числу отличных от нуля определителей порядка q, если ранг полной матрицы размерности равен k = q; числу комбинаций из m параметров по k, у которых ранг частичной матрицы размером k ´ q составляет k, если ранг полной матрицы размерности k < q.

В примере имеется 35 частичных матриц (C₇³ = 35) размером 3 ´ 4, каждая из которых соответствует комбинации 3-х параметров. Из них 22 матрицы имеют ранг равный трем, т.е. существуют 22 комбинации независимых параметров и, для четырех критериев подобия (K_p = 4) возможны 22 формы записи (F_p = 22).

V. Определение выражений для критериев подобия p₁, ..., p_m-k в какой-либо форме записи.

Для определения выражений критериев подобия в исходной зависимости f(P₁, ..., P_m) = 0

параметры P₁, ..., P_m перегруппировываются, и эта зависимость представляется в виде:

f(P₁, ..., P_i, ..., P_k; P_k+1, ..., P_s, ..., P_m) = 0,

где P₁, ..., P_i, ..., P_k - независимые параметры в какой-либо комбинации; P_k+1, ..., P_s, ..., P_m - остальные параметры с зависимыми размерностями.

Для группы независимых параметров u, R, C примера

f( u, R, C ; i, L, t, w ) = 0

Исходные формулы для определения выражений критериев подобия имеют вид (число критериев K_p = m - k, в примере K_p = 4):

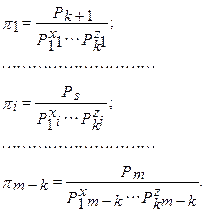
или, для примера

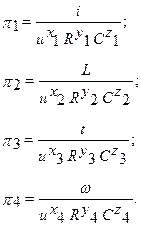
Для определения конкретного вида выражений критериев подобия p₁, ...., p_m-k необходимо найти значения показателей степеней x₁ - x_m-k, y₁ - y_m-k, z₁ - z_m-k при независимых параметрах P₁ - P_k (в примере x₁ - x₄, y₁ - y₄, z₁ - z₄ при параметрах u, R, C).

Критерии подобия - безразмерные величины, следовательно, размерности числителей и знаменателей в выражениях для критериев подобия одинаковы, отсюда, для p_s можно записать

[P_s] = [P₁]^xi ... [P_k]^zi

или

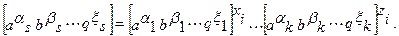
В примере для p₁ соотношение имеет вид

[i] = [u]^xi [R]^yi [C]^zi

или

[L⁰M⁰T⁰I¹] = [L²M¹T^-3I^-1] ^x1 [L²M¹T^-3I^-2] ^y1 [L^-2M^-1T⁴I²] ^z1.

Далее получаем систему из q уравнений с k = q неизвестными xi, ..., zi при a, b, ..., q соответственно. Система получается путем приравнивания показателей степеней при одноименных единицах измерения a, b, ..., q в левой части выражения для P_s и в правой части, записанной в виде произведения формул размерностей независимых параметров:

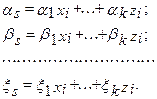
В примере для p₁ система уравнений имеет вид:

0 = 2x₁ + 2y₁ - 2 z₁;

0 = x₁ + y₁ - z₁;

0 = -3x₁ - 3y₁ + 4z₁;

1 = - x₁ - 2 y₁ + 2z₁ .

Решение системы дает x₁ = 1, y₁ = -1, z₁ = 0. Аналогично составляются и решаются системы для других неизвестных, окончательно:

x₁ = 1, x₂ = 0, x₃ = 0, x₄ = 0;

y₁ = -1, y₂ = 2, y₃ = 1, y₄ = -1;

z₁ = 0, z₂ = 1, z₃ = 1, z₄ = -1.

После определения значений степеней при независимых параметрах выражения критерия подобия записываются в окончательном виде.

Для рассматриваемого примера окончательные выражения для критериев подобия в форме записи, соответствующей независимым переменным u, R, C, будут иметь вид:

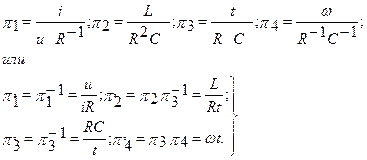
Кроме этой записи, можно определить выражения для критериев подобия и в любой другой форме записи, соответствующей иному составу группы независимых параметров P₁ - P_k.

В примере возможна еще 21 форма записи (F_p = 22) критериев подобия.

VI. Представление описания исследуемого процесса в виде критериального уравнения.

Исследуемый процесс представляется функциональной зависимостью между найденными критериями подобия

y( p₁, p₂, ..., p_i, ..., p_m-k ) = 0.

При этом следует учитывать, что один из критериев подобия (определяемый) обязательно является функцией остальных (определяющих или независимых) критериев подобия и, следовательно, автоматически выполняется при соблюдении независимых критериев подобия, можно окончательно записать критериальное уравнение в виде

p₁ = F(p₂, ¼, p_i, ¼, p_m-k),

уменьшив таким образом число величин, определяющих характер исследуемого процесса с m до (m - k - 1).

В примере m = 7, m - k - 1 = 3, а критериальное уравнение имеет вид

p₁ = F(p₂, p₃, p₄ ),

где для группы независимых параметров u, R, C будет p₁ = i/(uR^-1).