Интегральная теорема Лапласа. Пусть производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0<р<1)
Пусть производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0<р<1). Как вычислить вероятность того, что событие А появится в n испытаниях не менее k1 и не более k2 раз, т.е. Pn(k1,k2) (для кратности говорят «от k1 до k2 раз)? На этот вопрос дает ответ интегральная теорема Лапласа.
Теорема. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(k1,k2) того, что событие А появится в n испытаниях от k1 до k2 раз, приближенно равна определенному интегралу
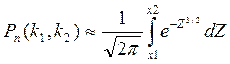(1.40)
где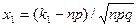 
и 
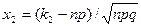
При решении задач пользуются специальными таблицами, так как неопределенный интеграл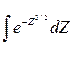 
не выражается через элементарные функции. Таблица для интеграла Ф(х) = 
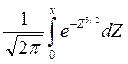(интегральная функция Лапласа) приводится в приложениях к учебникам по теории вероятностей (например, Гмурман, приложение 2, с.462). В таблицах приводятся значения Ф(х) для положительных значений х и для х=0; для х<0 пользуются той же таблицей [функция Ф(х) нечетна, т.е. Ф(-х)=-Ф(х)]. В таблицах приводятся значения интеграла лишь до х=5, так как для х >5можно принять Ф(х) = 0,5. Значение искомой вероятности равно
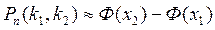
Пример 1.68. Вероятность того, что деталь не прошла проверку качества, равна р=0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непригодных от 70 до 100 деталей.
Решение. По условию, р=0,2; q=0,8; n=400; k1=70; k2=100. Воспользуемся интегральной формулой Лапласа:
Р400(70, 100) ≈ Ф(х2) – Ф(х1).
Вычислим нижний и верхний пределы интегрирования:
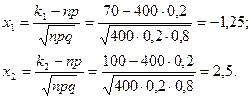
Таким образом, имеем Р400(70, 100)=Ф(2,5)-Ф(-1,25)=Ф(2,5)+Ф(1,25).
По таблице (приложение2, Гмурман) находим: Ф(2,5) = 0,4938; Ф(1,25) = 0,3944.
Искомая вероятность Р400(70, 100)= 0,4938+0,3944 = 0,8882.
Домашнее задание: ДР-15( №3.28,Зарубин, стр. 117)
Дата добавления: 2015-10-30; просмотров: 722;