Примеры непосредственного вычисления вероятностей

Пример 1.34. Набирая номер телефона, абонент забыл одну цифру и набрал ее наугад. Найти вероятность того, что набрана нужная цифра.

Решение. Обозначим через А событие — набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 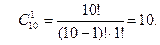Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует собы­тию А лишь один исход (нужная цифра лишь одна). Искомая веро­ятность равна отношению числа исходов, благоприятствующих со­бытию, к числу всех элементарных исходов:

Р (А) = 1/10.

Пример 1.35.Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры "различны, набрал их на­угад. Найти вероятность того, что набраны нужные цифры.

Решение. Обозначим через В событие — набраны две нужные цифры. Всего можно набрать столько различных цифр, сколько может быть составлено размещений из десяти цифр по две, т. е. 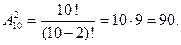Таким образом, общее число возможных элементар­ных исходов равно 90. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность равна отношению числа исходов, благо­приятствующих событию, к числу всех элементарных исходов: Р (В) = 1/90.

Пример 1.36.Брошены два игральных кубика. Найти вероятность того, что сумма выпавших очков равна 4 (событие А).

Решение. Общее число равновозможных исходов испытания равно 6∙6 = 36 (каждое число выпавших очков на одном кубике может сочетаться со всеми числами очков другого кубика). Среди этих исходов благоприятствуют событию А только 3 исхода: (I; 3), (3; I), (2; 2) (в скобках указаны числа выпавших очков). Следовательно, искомая вероятность

Р (А) = 3/36 =1/12.

Пример 1.37.В партии из 10 деталей 7 стандартных. Найти вероят­ность того, что среди шести взятых наугад деталей 4 стандартных.

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. числу сочетаний из 10 элементов по 6 элементов ( ).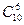

Определим число исходов, благоприятствующих интересующему нас событию А (среди шести взятых деталей 4 стандартных). Четыре стандартные детали можно взять из семи стандартных деталей 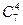спо­собами; при этом остальные 6 - 4 = 2 детали должны быть нестан­дартными; взять же 2 нестандартные детали из 10 - 7 = 3 нестандарт­ных деталей можно 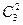способами. Следовательно, число благоприя­тствующих исходов равно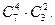

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

P(A) =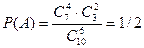

Домашнее задание: ДР-1, ДР-2 (задачи 1.20, 1.21/Письменный, с.29, 30)