Операции над событиями

События обозначаются заглавными буквами начала латинского алфавита A, B, C, D, …, снабжая их при необходимости индексами. Тот факт, что элементарный исход х содержится в событии А, обозначают .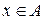

Для понимания удобна геометрическая интерпретация при помощи диаграмм Виенна: представим пространство элементарных событий Ω в виде квадрата, каждой точке которого соответствует элементарное событие. Случайные события А и В, состоящие из совокупности элементарных событий х_i и у_j, соответственно, геометрически изображаются в виде некоторых фигур, лежащих в квадрате Ω (рис. 1-а, 1-б).

Пусть опыт состоит в том, что внутри квадрата, изображенного на рисунке 1-а, выбирается наугад точка. Обозначим через А событие, состоящее в том, что {выбранная точка лежит внутри левой окружности} (рис.1-а), через В – событие, состоящее в том, что {выбранная точка лежит внутри правой окружности} (рис. 1-б).

Достоверному событию благоприятствует любое 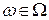, поэтому достоверное событие будем обозначать тем же символом Ω.

Два события тождественны друг другу (А=В) тогда и только тогда, когда эти события состоят из одних и тех же элементарных событий (точек).

Суммой (или объединением) двух событий А и В называется событие А+В (или 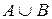), происходящее тогда и только тогда, когда происходит или А, или В. Сумме событий А и В соответствует объединение множеств А и В (рис. 1-д).

Пример 1.15. Событие, состоящее в выпадении четного числа, является суммой событий: выпало 2, выпало 4, выпало 6. То есть, {х=четное }= {х=2}+{х=4 }+{х=6 }.

Отметим очевидные соотношения: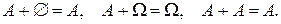

Произведением (или пересечением) двух событий А и В называется событие АВ (или 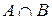), происходящее тогда и только тогда, когда происходит и А, и В. Произведению событий А и В соответствует пересечение множеств А и В (рис. 1-е).

Пример 1.16. Событие, состоящее в выпадении 5, является пересечением событий: выпало нечетное число и выпало больше 3-х, то есть, A{x=5}=B{x-нечетное}∙C{x>3}.

Отметим очевидные соотношения: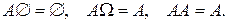

Событие 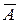называется противоположным к А, если оно происходит тогда и только тогда, когда А не происходит. Геометрически – это множество точек квадрата, не входящее в подмножество А (рис. 1-в). Аналогично определяется событие 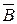(рис. 1-г).

Пример 1.14.. События, состоящие в выпадении четного и нечетного чисел, - события противоположные.

Отметим очевидные соотношения: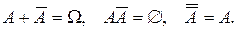

Два события называются несовместными, если их одновременное появление в опыте невозможно. Следовательно, если А и В несовместны, то их произведение – невозможное событие: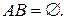

Введенные ранее элементарные события, очевидно, попарно несовместны, то есть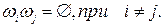

Пример 1.17. События, состоящие в выпадении четного и нечетного чисел, - события несовместные.

А В 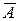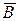а) б) в) г)

А+В АВ 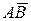или А\В В\А или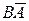

д) е) ж) з)

Рис. 1. Диаграммы Виенна

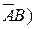Разностью событий А и В называется событие А\В (или ), происходящее тогда и только тогда, когда происходит А, но не происходит В (рис. 1-ж). Аналогично определяется событие В\А (или (рис.1-з).

Отметим очевидные соотношения: 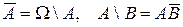(рис. 1-г).

Так как разность событий можно выразить с помощью операций отрицания и произведения, пользоваться разностью событий в дальнейшем не будем.

Введенные выше операции сложения и умножения обладают следующими свойствами: А+В=В+А, АВ=ВА, А(В+С)=АВ+АС, А(ВС)=(АВ)С.

Пример 1.18. Производится два выстрела по цели. Пусть событие А –{попадание в цель при первом выстреле}, В ––{попадание при втором выстреле}, тогда 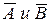- промахи, соответственно, при первом и втором выстрелах. Обозначим: событие С –{поражение цели} и примем, что для этого достаточно хотя бы одного попадания. Требуется выразить событие С через события А и В.

Решение. Цель будет поражена в следующих случаях: попадание при первом и промах при втором; промах при первом и попадание при втором; попадание при первом и втором выстрелах. Используя введенные выше операции, перечисленные варианты можно соответственно записать: 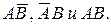интересующее нас событие заключается в наступлении или первого, или второго, или третьего вариантов (хотя бы одного), то есть

.

С другой стороны, событие 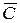, противоположное событию С, есть промах при двух выстрелах, то есть 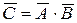, отсюда искомое событие С можно записать в виде 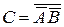. Возможность различного выражения искомого события часто оказывается полезной при решении задач.