Предмет и задачи теории вероятностей

До появления теории вероятностей как действительно общепризнанной теории в науке господствовал детерминизм, согласно которому осуществление определенных условий однозначно определяет результат. То есть, если будет осуществлена (реализована) определенная совокупность условий S, то некоторое событие А обязательно произойдет.

Классическим примером является механика: если известны начальное положение, скорость материальной точки и действующие силы, то можно определить ее дальнейшее движение. Еще пример: при нормальном атмосферном давлении и температуре 20°С вода будет находиться в жидком состоянии.

Развитие этого подхода привело знаменитого французского математика и механика Пьера Лапласа к своеобразной механистической модели мироздания.

Однако практика показала, что этот подход далеко не всегда применим. Во многих случаях предсказать наступление данного явления даже при реализации соответствующих условий невозможно: оно может произойти, а может и не произойти. Например, в механике мы никогда абсолютно точно не знаем начальных параметров движущегося тела, действующих на него в начале и в процессе движения сил, следовательно, и в прогнозировании дальнейшего движения тела возникает некоторая неопределенность.

Приведем более простые примеры: а) при бросании монеты невозможно предсказать, какой стороной (гербом или цифрой) кверху она упадет. То есть, событие, что "при бросании монеты выпадет герб" заранее предсказать нельзя: оно может произойти или не произойти; б) продолжительность жизни определенного человека заранее неизвестна. То есть, событие, заключающееся в том, конкретный человек проживет какое определенное количество лет, может произойти или не произойти.

Событие, которое при осуществлении совокупности условий S может произойти, либо не произойти называют случайным событием

То есть, событие {"при бросании монеты выпал герб"}- случайное.

Каждое случайное событие, в частности выпадение "герба", является следствием многих случайных причин, характер действия которых вследствие недостаточной их изученности не поддается точному учету. Например, выпадение «герба» есть следствие действия ряда факторов, а именно, силы, с которой брошена монета; точки приложения и направления действия этой силы, формы и симметричности распределения материала монеты, состояния атмосферы в зоне «полета» монеты и другие. Предсказать заранее характер изменения этих параметров и учесть их влияние на движение монеты практически невозможно, вследствие чего невозможно заранее предсказать, какой стороной кверху упадет монета. Число таких примеров из различных областей практической деятельности человека можно неограниченно продолжать.

Дальнейшее развитие науки, в особенности физики, еще более поставило под вопрос единственность детерминистического подхода к изучению многих явлений. Более того, многие выдающиеся естествоиспытатели и философы современности склонны даже считать, что все без исключения законы природы на самом деле имеют вероятностный характер. Еще больше сомнений в справедливости детерминизма дало развитие естествознания (генетика, медицина и др.) и общественных наук (экономика, в частности страховое дело, демография и многие другие).

Дальнейшие исследования показали, что результаты индивидуальных случайных опытов непредсказуемы. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет,- она просто не в силах это сделать. По-иному обстоит дело, если рассматриваемые случайные события повторяются многократно при осуществлении одних и тех же условий S, т.е. если речь идет о массовых однородных случайных событиях.

Оказалось, что достаточно большое число однородных массовых случайных событий независимо от их конкретной природы подчиняется определенным закономерностям, называемым вероятностными закономерностями. Установлением таких закономерностей и занимается теория вероятностей.

Таким образом, предметом теории вероятностей является изучение вероятностных закономерностей, возникающих при массовых однородных опытах.

Знание закономерностей, которым подчиняются массовые однородные события, позволяют предвидеть, как эти события будут протекать. Например, как было уже сказано, если бросить одну монету, никто не сможет предсказать, какой стороной она упадет кверху, но если бросить две тонны монет, то каждый скажет, что примерно половина из них, т.е., одна тонна упадет кверху гербом.

Во всех случаях, когда применяются вероятностные методы исследования, их цель состоит в том, чтобы, минуя слишком сложное (и часто практически невозможное) изучение отдельного явления, обусловленного очень большим количеством случайных факторов, обратиться непосредственно к законам, управляющим массами случайных явлений. Изучение этих законов позволяет не только осуществить научный прогноз в своеобразной области случайных явлений, но в ряде случаев помогает целенаправленно влиять на ход случайных явлений, контролировать их, ограничивать сферу действий случайности.

В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу.

Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей.

Вероятностный метод в науке не противопоставляет себя классическому методу точных наук, а является его дополнением, позволяющим глубже анализировать явление с учетом присущих ему элементов случайностей, позволяющим не только выявить основные закономерности, но и провести анализ возможных отклонений от них.

Необходимо отметить, что в последнее время находит все большее признание другой взгляд, согласно которому методы и результаты теории вероятностей применимы не только к массовым, но и к единичным, даже к уникальным явлениям и сооружениям. Действительно, во-первых, даже уникальное сооружение, как правило, состоит из массовых элементов, во-вторых, вероятность есть некоторая объективная мера возможности наступления события. Эта мера сохраняет свой смысл независимо от того, является это событие многократно воспроизводимым или единичным. Покупая единственный телевизор, мы естественно выбираем более надежную марку; возникновение жизни на Земле – уникальное явление, но астрономы говорят о вероятности этого в нашей и других галактиках.

Зарождение теории вероятностей, формулирование ее основных положений относится к середине XVII века и связано с работами Блеза Паскаля (1623-1662), Пьера Ферма (1601-1665), Христиана Гюйгенса (1629-1695) и других в области теории азартных игр.

Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654-1705). Доказанная им теорема, получившая впоследствии название "Закона больших чисел", была первым теоретическим обоснованием накопленных ранее фактов.

Дальнейшее развитие теории вероятностей связано с именами Абрахама де Муавра (1667-1754), Пьера Симона Лапласа (1749-1827), Карла Фридриха Гаусса (1777-1855), Симеона Дени Пуассона (1781-1840) и др.. Ими сформулированы и доказаны основные теоремы теории вероятностей, разработаны методы решения важных практических задач.

Наиболее плодотворный период развития теории вероятностей связан с именами Пафнутия Львовича Чебышева (1821-1894) и его учеников А. М. Ляпунова (1857-1918), А. А. Маркова (1856-1922). В этот период теория вероятностей становится стройной математической наукой.

Ее последующее развитие во многом обязано советским математикам С.Н. Бернштейну, В.И. Романовскому, А.Н. Колмогорову, А.Я. Хинчину, Б.В. Гнеденко, Н.В. Смирнову и др., внесшим значительный вклад в создание новых ветвей теории вероятностей.

Случайные события

Основные понятия теории вероятностей

Теория вероятностей – это математическая наука, изучающая закономерности, возникающие при массовых случайных явлениях или в массовых однородных опытах.

Все наблюдаемые нами события (явления) можно разделить на следующие три вида: достоверные, невозможные и случайные.

Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S.

Пример 1.1. Если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20°, то событие {вода в сосуде находится в жидком состоянии} есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют совокупность условий S.

Пример 1.2. Событие, состоящее в выпадении не более 6 очков при бросании одного игрального кубика, есть событие достоверное.

Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S.

Пример 1.3. Если будет осуществлена совокупность условий предыдущего примера, событие {вода в сосуде находится в твердом состоянии} заведомо не произойдет. Оно в данном случае событие невозможное.

Пример 1.4. Событие, состоящее в выпадении 10 очков при бросании одной игрального кубика, есть событие невозможное.

Невозможному событию соответствует пустое множество, поэтому его будем обозначать символом .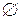

Случайным называют событие, которое при осуществлении совокупности условий S может произойти, либо не произойти.

Пример 1.5. Если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись. Поэтому событие {при бросании монеты выпал герб}- случайное.

Для обозначения случайных событий используются большие буквы начала латинского алфавита А, В, С, …, снабжая их при необходимости индексами.

Исходными понятиями теории вероятностей являются понятия стохастического эксперимента, случайного события и вероятности случайного события.

Стохастическим называется эксперимент, результат которого заранее (до его проведения) предугадать нельзя. Часто вместо стохастического эксперимента говорят об испытании, опыте.

Пример 1.6. Рассмотрим опыт с бросанием игрального кубика с цифрами от 1 до 6 на гранях. Результатом этого стохастического эксперимента/опыта может быть появление одного из чисел 1, 2, 3, 4, 5, 6. Можно рассматривать и другие события, заключающиеся, например, в том, что выпадет четная/нечетная цифра, сумма выпавших чисел равна пяти, четная, делится на три и т.д.

Элементарным исходом называется элементарное, неразложимое событие. Любое событие может быть разложено на элементарные исходы; иначе говоря, событие есть совокупность элементарных исходов.

Пример 1.7. Событие, заключающееся в том, что сумма очков, выпавших при бросании двух игральных кубиков, равна шести, может состоять из элементарных событий, заключающихся в выпадении (1, 5), или (2, 4), или (3, 3), или 4, 2), или (5, 1). То есть, событие {сумма очков равна шести} разлагается на пять элементарных исходов.

Элементарные события обладают следующими свойствами:

· взаимно исключают друг друга, и в результате опыта обязательно происходит одно из этих элементарных событий;

· каково бы ни было случайное событие А, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие А.

Элементарные события обозначают греческой буквой ω, снабжаемой при необходимости индексом, или строчными буквами конца латинского алфавита: x, y, z, …, снабжаемыми при необходимости индексами. Совокупность элементарных событий обозначают Ω и называют пространством элементарных событий.

Пример 1.8. В рассмотренном ранее примере 1.5 элементарными событиями ω_i можно считать появление любого числа от 1 до 6. Очевидно, что всего имеется 6 элементарных событий. Выбор элементарных событий определяется неоднозначно, чем можно пользоваться при решении задач.

В дальнейшем, вместо того чтобы говорить "совокупность условий S осуществлена", будем говорить кратко: "произведено "испытание". Таким образом, событие будет рассматриваться как результат испытания.

Пример 1.9. Стрелок стреляет по мишени, разделенной на четыре области. Выстрел – это испытание. Попадание в определенную область мишени - событие. В урне имеются цветные шары. Из урны наугад берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета - событие.