Определение вероятности

Ясно, что каждое событие обладает той или иной степенью возможности своего наступления (своей реализации). Чтобы количественно сравнивать между собой события по степени их возможности, очевидно, нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое число называется вероятностью события.

Вероятность события – есть численная мера степени объективной возможности наступления этого события.

Рассмотрим стохастический эксперимент и случайное событие А, наблюдаемое в этом эксперименте. Повторим этот эксперимент n раз и пусть m(A) – число экспериментов, в которых событие А произошло.

Отношение 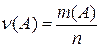(1.1)

называется относительной частотой события А в проведенной серии экспериментов.

Легко убедиться в справедливости свойств: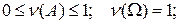

если А и В несовместны (АВ= 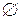), то ν(А+В) = ν(А) + ν(В) (1.2)

Относительная частота определяется только после проведения серии экспериментов и, вообще говоря, может меняться от серии к серии. Однако опыт показывает, что во многих случаях при увеличении числа опытов относительная частота приближается к некоторому числу. Этот факт устойчивости относительной частоты неоднократно проверялся и может считаться экспериментально установленным.

Пример 1.19.. Если бросить одну монету, никто не сможет предсказать, какой стороной она упадет кверху. Но если бросить две тонны монет, то каждый скажет, что примерно одна тонна упадет кверху гербом, то есть относительная частота выпадения герба примерно равна 0,5.

Если при увеличении числа опытов относительная частота события ν(А) стремится к некоторому фиксированному числу, то говорят, что событие А статистически устойчиво, а это число называют вероятностью события А.

Вероятностью события А называется некоторое фиксированное число Р(А), к которому стремится относительная частота ν(А) этого события при увеличении числа опытов, то есть,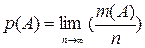

Это определение называют статистическим определением вероятности.

Рассмотрим некий стохастический эксперимент и пусть пространство его элементарных событий состоит из конечного или бесконечного (но счетного) множества элементарных событий ω₁, ω₂, …, ω_i, … . предположим, что каждому элементарному событию ω_i прописан некоторое число - р_i, характеризующее степень возможности появления данного элементарного события и удовлетворяющее следующим свойствам:

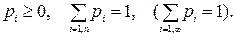(1.3)

Такое число p_i называется вероятностью элементарного события ω_i.

Пусть теперь А- случайное событие, наблюдаемое в этом опыте, и ему соответствует некоторое множество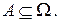

В такой постановке вероятностью события А называют сумму вероятностей элементарных событий, благоприятствующих А (входящих в соответствующее множество А):

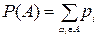(1.4)

Введенная таким образом вероятность обладает теми же свойствами, что и относительная частота, а именно:

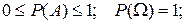и если АВ= 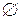(А и В несовместны),

то P(А+В) = P(А) + P(В)

Действительно, согласно (1.4)

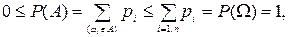
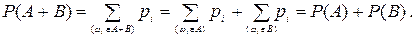
В последнем соотношении мы воспользовались тем, что ни одно элементарное событие не может благоприятствовать одновременно двум несовместным событиям.

Особо отметим, что теория вероятностей не указывает способов определения р_i, их надо искать из соображений практического характера или получать из соответствующего статистического эксперимента.

В качестве примера рассмотрим классическую схему теории вероятностей. Для этого рассмотрим стохастический эксперимент, пространство элементарных событий которого состоит из конечного (n) числа элементов. Предположим дополнительно, что все эти элементарные события равновозможны, то есть вероятности элементарных событий равны p(ω_i)=p_i=p. Отсюда следует, что

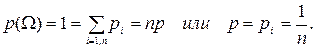
Пример 1.20. При бросании симметричной монеты выпадение герба и «решки» равновозможны, их вероятности равны 0,5.

Пример 1.21. При бросании симметричного кубика все грани равновозможны, их вероятности равны 1/6.

Пусть теперь событию А благоприятствует m элементарных событий, их обычно называют исходами, благоприятствующими событию А. Тогда

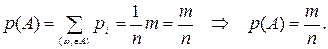(1.5)

Получили классическое определение вероятности: вероятность Р(А) события А равна отношению числа исходов, благоприятствующих событию А, к общему числу исходов

Пример 1.22. В урне лежит m белых шаров и n черных. Чему равна вероятность вытащить белый шар?

Решение. Всего элементарных событий m+n. Они все равновероятны. Благоприятствующих событию А из них m. Следовательно, .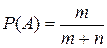

Из определения вероятности вытекают следующие ее свойства:

Свойство 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует собы­тию. В этом случае т=п, следовательно,

P(A)=m/n=n/n=1. (1.6)

Свойство 2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае т = 0, следовательно, P(A)=m/n=0/n=0. (1.7)

Свойство 3.Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испы­тания. То есть, 0≤m≤n, значит, 0≤m/n≤1, следовательно, вероятность любого события удовлетворяет двойному неравенству 0≤P(A) ≤1. (1.8)

Сопоставляя определения вероятности (1.5) и относительной частоты (1.1), заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.

Однако, вычисление вероятности требует наличия предварительной информации о количестве или вероятностях благоприятствующих данному событию элементарных исходов. В случае отсутствия такой предварительной информации для определения вероятности прибегают к эмпирическим данным, то есть, по результатам стохастического эксперимента определяют относительную частоту события.

Пример 1.23. Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80 случайно отобранных деталей. Относительная частота появления нестандартных деталей r (А) = 3/80.

Пример 1.24. По цели .произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Относительная частота поражения цели. r (А) =19/24.

Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Оказалось, что это постоянное число можно принять за приближенное значение вероятности.

Подробнее и точнее связь между относительной частотой и вероятностью будет изложена далее. Теперь же проиллюстрируем свойство устойчивости на примерах.

Пример 1.25. По данным шведской статистики, относительная частота рождения девочек за 1935 г. по месяцам характеризуется сле­дующими числами (числа расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0.471; 0,478; 0,482; 0.462; 0,484; 0,485; 0,491; 0,482; 0,473

Относительная частота колеблется около числа 0,481, которое можно принять за приближеннее значение вероятности рождения девочек.

Заметим, что статистические данные различных стран дают примерно то же значение относительной частоты.

Пример 1.26. Многократно проводились опыты бросания монеты, в которых подсчитывали число появление «герба». Результаты нескольких опытов приведены в таблице.

Здесь относительные частоты незначительно отклоняются от числа 0,5, причем тем меньше, чем больше число испытаний. Например, при 4040 испытаниях отклонение равно 0,0069, а при 24000 испытаниях - лишь 0,0005. Приняв во внимание, что вероятность появления «герба» при бросании монеты равна 0,5, мы вновь убеждаемся, что относительная частота колеблется около вероятности.