Формулы комбинаторики.

Для решения задач, связанных с непосредственным вычислением вероятностей, разработана техника подсчета всевозможных комбинаций предметов, в которых используются формулы комбинаторики.

Комбинаторика – раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами.

Другими словами, целью комбинаторного анализа является построение некоторой конструкции, называемой комбинаторной конструкцией, подчиненной определенным условиям, которые можно составить из элементов заданного конечного множества независимо от природы этих элементов.

Приведем наиболее употребительные из них

1. Размещениями называют комбинации, составленные из п различных элементов по m элементов, которые от­личаются либо составом элементов, либо их порядком.

Пусть из некоторого множества, состоящего из n различимых элементов, отбирается в определенном порядке m. Для подсчета возможных вариантов заметим, что первый элемент можно выбрать n способами, второй – (n-1) способами, …, m-ый вариант – (n-m+1) способами. Согласно правилу произведения общее число вариантов будет равно n∙(n-1) ∙ … ∙(n-m+1). Такие комбинации называют размещениями, число всех возможных размещений

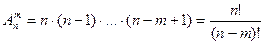, (1.9)

где n! = 1∙2∙3∙. . . ∙n (читается n-факториал).

Пример 1.27. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2, если имеет значение цвет флажка в каждой руке?

Решение. Искомое число сигналов

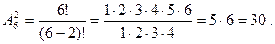
Пример 1.28. Сколькими способами из 20 членов правления фирмы можно отобрать трех для замещения вакансий вице-президентов, отвечающих соответственно за производство, финансы, реализацию продукции?

Решение. Поскольку порядок при таком выборе играет существенную роль, число вариантов равно

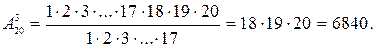
2. Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающихся только порядком их расположения.

Число всех возможных перестановок равно числу размещений при n=m, то есть 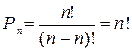(1.10)

Здесь учтено, что 0! = 0∙1 = 1.

Пример 1.29. Сколько трехзначных чисел можно составить из цифр 1 , 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение. Искомое число трехзначных чисел

Р₃ = 3! = 1∙2∙3 = 6.

Это 1, 2, 3 или 1, 3, 2, или 2, 1, 3, или 2, 3, 1, или 3, 1, 2, или 3, 2, 1.

Если в размещениях порядок отбираемых m элементов из n не играет роли, то говорят о числе сочетаний из n элементов по m.

3. Сочетаниями называют комбинации, составленные из n различных элементов по т элементов, которые отли­чаются хотя бы одним элементом. Число сочетаний

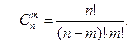(1.11)

Пример 1.30. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2, если цвет флажка в каждой руке не имеет значения?

Решение. Искомое число сигналов

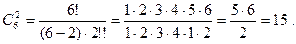
Пример 1.31. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение. Искомое число способов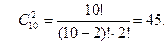

Пример 1.32. Сколькими способами можно из 20 присяжных заседателей отобрать трех для участия в судебном процессе.

Решение. Поскольку несущественно, в каком порядке отобраны кандидатуры, число вариантов равно

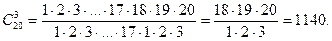
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством 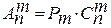(1.11-а)

Примечание 1. Выше предполагалось, что все п элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, п₂ элементов другого вида и т. д, то число перестановок с повторениями

P_n(n₁, п₂, … ) = 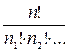(1.12)

где n₁ + n₂ + . . . = п.

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, другой объект В может быть выбран п способами, то выбрать либо А, либо В можно т + п способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов т способами и после каждого такого выбора объект В можно выбрать п спо­собами, то пара объектов (А, В) в указанном порядке может быть выбрана тп способами.

Примечание 2. При большом n подсчет числа вариантов по приведенным выше формулам требует громоздких вычислений n!. В этом случае пользуются асимптотической формулой Стирлинга

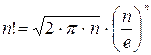(1.13)

Пример 1.33.Среди K поставленных единиц данного товара S не удовлетворяют предъявляемым условиям. Найти вероятность того, что среди k≤K, отобранных для выборочного контроля качества, равно s≤S не будут удовлетворять этим требованиям (этот опыт называется «контролем качества»).

Решение. Опыт в случайном отборе отборе k образцов. Следовательно, исходы этого испытания равновозможны и общее число вариантов отбора равно 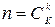. Событие А состоит в том, что из k отобранных ровно s не будут удовлетворять этим требованиям. Число исходов, благоприятствующих А, согласно правилу произведения равно 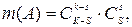здесь первый множитель дает число вариантов отбора хороших, а второй – плохих образцов. Отсюда искомая вероятность

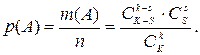(1.14)