Равную нулевому вектору.

Упражнение. Докажите, что всякая часть линейно независимого набора векторов является линейно независимым набором.

Геометрический смысл линейной зависимости векторов вR³, интерпретируемых как направленные отрезки, поясняют следующие теоремы.

Теорема 3.2. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.

Теорема 3.3. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.

Теорема 3.4. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.

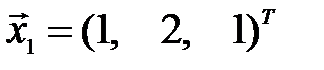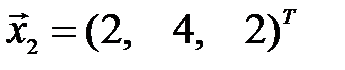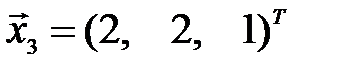Пример 3.8. Выяснить, являются ли векторы , и линейно зависимыми.

Решение. Поскольку 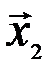является линейной комбинацией векторов 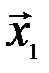и 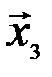: 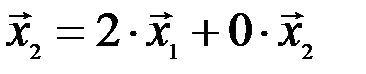, то по теореме 3.1 эти векторы линейно зависимые.

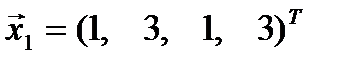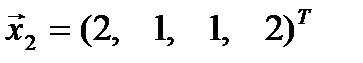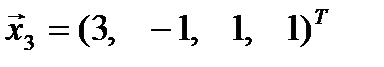Пример 3.9 Выяснить, являются ли векторы , и линейно зависимыми.