Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении
 Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс
Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс 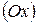 , вторая – осью ординат
, вторая – осью ординат 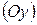 , третья – осью аппликат
, третья – осью аппликат 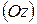 ; точка
; точка 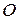 ‑ начало координат (Рис. 4.4).
‑ начало координат (Рис. 4.4).

Положение координатных осей можно задать с помощью единичных векторов 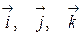 , направленных соответственно по осям
, направленных соответственно по осям 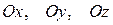 . Векторы
. Векторы 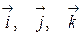 называются основными или базисными ортами и определяют базис
называются основными или базисными ортами и определяют базис 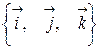 в трехмерном пространстве.
в трехмерном пространстве.
Пусть в пространстве дана точка 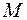 . Проектируя ее на ось
. Проектируя ее на ось 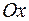 , получим точку
, получим точку 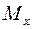 . Первой координатой
. Первой координатой 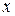 или абсциссой точки
или абсциссой точки 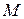 называется длина вектора
называется длина вектора 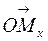 , взятая со знаком плюс, если
, взятая со знаком плюс, если 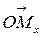 направлен в ту же сторону, что и вектор
направлен в ту же сторону, что и вектор 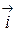 , и со знаком минус ‑ если в противоположную. Аналогично проектируя точку
, и со знаком минус ‑ если в противоположную. Аналогично проектируя точку 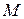 на оси
на оси 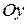 и
и 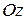 , определим ее ординату
, определим ее ординату 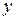 и аппликату
и аппликату 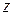 . Тройка чисел
. Тройка чисел 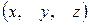 взаимно однозначно соответствует точке
взаимно однозначно соответствует точке 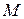 .
.
Система координат называется правой, если вращение от оси 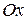 к оси
к оси 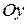 в ближайшую сторону видно с положительного направления оси
в ближайшую сторону видно с положительного направления оси 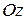 совершающимися против часовой стрелки, и левой, если вращение от оси
совершающимися против часовой стрелки, и левой, если вращение от оси 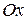 к оси
к оси 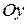 в ближайшую сторону видно совершающимися по часовой стрелке.
в ближайшую сторону видно совершающимися по часовой стрелке.
Вектор 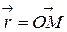 , направленный из начала координат в точку
, направленный из начала координат в точку 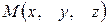 называется радиус-вектором точки
называется радиус-вектором точки 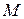 , т.е.:
, т.е.:
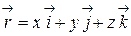
| (4.6) |
Если даны координаты точек 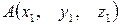 и
и 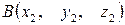 , то координаты вектора
, то координаты вектора 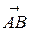 получаются вычитанием из координат его конца
получаются вычитанием из координат его конца 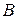 координат начала
координат начала 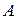 :
: 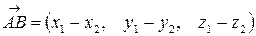 или
или 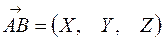 .
.
Следовательно, по формуле (4.5):
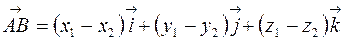 или или
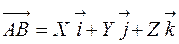
| (4.7) |
При сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число все его координаты умножаются на это число.
Длина вектора 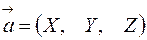 равна квадратному корню из суммы квадратов его координат.
равна квадратному корню из суммы квадратов его координат.
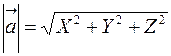 . .
| (4.8) |
Длина вектора  , заданного координатами своих концов, т.е. расстояние между точками
, заданного координатами своих концов, т.е. расстояние между точками 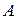 и
и  вычисляется по формуле:
вычисляется по формуле:
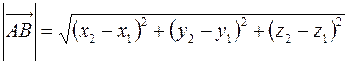 . .
| (4.9) |
Если 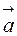 и
и 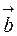 коллинеарны, то они отличаются друг от друга скалярным множителем. Следовательно, у коллинеарных векторов координаты пропорциональны:
коллинеарны, то они отличаются друг от друга скалярным множителем. Следовательно, у коллинеарных векторов координаты пропорциональны:
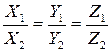 . .
| (4.10) |
Пусть точка 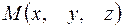 делит отрезок между точками
делит отрезок между точками 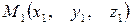 и
и 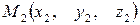 в отношении
в отношении 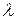 , тогда радиус-вектор точки
, тогда радиус-вектор точки 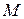 выражается через радиусы-векторы
выражается через радиусы-векторы 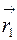 и
и 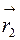 его концов по формуле:
его концов по формуле: 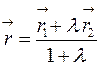 .
.
Отсюда получаются координатные формулы:
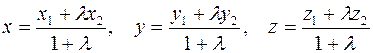 .
.
В частности, если точка 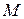 делит отрезок
делит отрезок 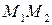 пополам, то
пополам, то 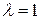 и
и 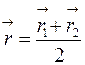 , т.е.
, т.е. 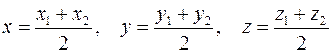 .
.
Дата добавления: 2015-10-09; просмотров: 1082;
