Выражение скалярного произведения через координаты

Пусть заданы два вектора

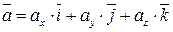и .

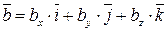Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов , , :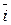

,

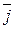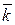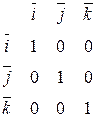
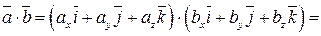
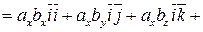
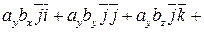
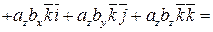
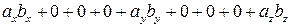т.е. .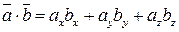

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Угол между векторами

Определение угла 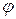между ненулевыми векторами и :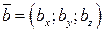

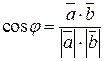, т.е. .

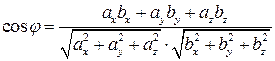Отсюда следует условие перпендикулярности ненулевых векторов 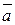и :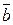

.

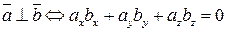Проекция вектора на заданное направление

Нахождение проекции вектора 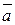на направление, заданное вектором 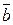, может осуществляться по формуле

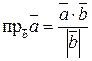
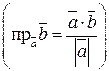, т.е. .

Работа постоянной силы

Пусть материальная точка перемещается прямолинейно из положения 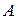в положение 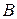под действием постоянной силы 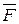, образующей угол 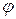с перемещением .

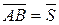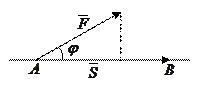
Из физики известно, что работа силы 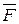при перемещении 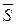равна

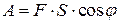, т.е. .

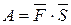Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.