Характеристики МПС с общей памятью

Будем рассматривать мультипроцессорную систему (МПС) с общей памятью, в которой размещаются все программы и данные, используемые в процессе функционирования системы. Такая организация типична для управляющих систем, жесткие ограничения на время реакции которых исключают возможность размещения информации во внешней памяти. Будем считать, что в МПС используются одинаковые процессоры, т.е. МПС – однородная система. Наличие общей оперативной памяти, в которой размещается вся необходимая информация, и однородность системы позволяют выполнять любую программу на любом процессоре, т.е. любой процессор может принять на обслуживание любую заявку. Режим работы МПС, при котором каждый из процессоров может обслуживать любую заявку, называется режимом разделения нагрузки. При этом режиме каждый из N процессоров принимает на обслуживание N-ю часть заявок, т.е. N-ю часть общей нагрузки.

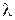Модель МПС с общей памятью. Процесс обслуживания заявок в режиме разделения нагрузки можно рассматривать как процесс функционирования одной многоканальной системы массового обслуживания (рис. 3.38) с интенсивностью входящего потока, общей очередью О, заявки из которой выбираются в порядке поступления их в систему, и средней длительностью обслуживания заявки каждым из процессоров Пр₁,…, Пр_N равной 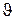. Заявка, поступающая в систему, содержащую N процессоров, при наличии хотя бы одного свободного процессора немедленно принимается последним на обслуживание. Если все процессоры заняты обслуживанием ранее поступивших заявок, поступающая заявка размещается в очереди.

Определим характеристики МПС на основе модели рис. 3.38.

Пусть в МПС поступает М потоков с интенсивностями 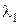,…, 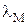. Обслуживание заявок сводится к выполнению соответствующих программ, средние трудоемкости которых равны 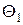,…, 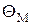операций в расчете на один прогон программы. Примем, что обслуживание заявок выполняется на основе дисциплины FIFO. В таком случае можно считать, что система обслуживает однородный поток заявок, поступающих с интенсивностью

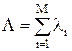(3.45)

Для обслуживания любой заявки из суммарного потока требуется в среднем

(3.46)

процессорных операций.

Примем, что заявка, поступившая на обслуживание, захватывает процессор до полного завершения обслуживания. В таком случае средняя длительность обслуживания заявки процессором с быстродействием В равна 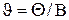и интенсивность обслуживания заявок одним процессором .

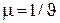Параметры системы 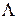, N и 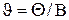должны отвечать условию существования стационарного режима, при котором в очереди пребывает конечное число заявок и, следовательно, конечны времена ожидания и пребывания заявок. На каждый из процессоров поступает N-я доля заявок и, следовательно, отдельный процессор обслуживает поток с интенсивностью 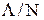. Загрузка процессора

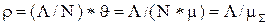(3.47)

где 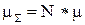- суммарная интенсивность обслуживания заявок N-процессорной системой.

Стационарный режим существует, если 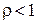. Следовательно, параметры МПС должны отвечать соотношению .

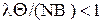Характеристики системы можно получить в явной аналитической форме, если принять предположение о том, что входящий поток заявок – пуассоновский и длительность обслуживания распределена по экспоненциальному закону со средним .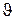

В теории массового обслуживания доказывается, что при указанных предположениях вероятность пребывания в системе N=0,1,2,… заявок, обслуживаемых процессорами и стоящих в очереди

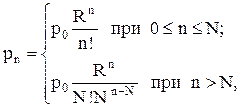(3.48)

где

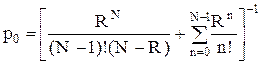(3.49)

- вероятность того, что в системе нет ни одной заявки, т.е. все N процессоров простаивают; R – суммарная загрузка N-канальной системы равная

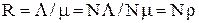(3.50)

Суммарная загрузка R в отношении N-канальной системы массового обслуживания определяет среднее число каналов, которые заняты обслуживанием заявок. Для стационарного режима R<N. С учетом 3.50 выражения 3.48 и 3.49 можно представить в виде:

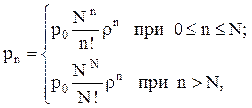(3.51)

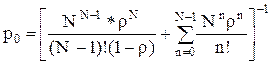(3.52)

где 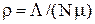– загрузка процессора N-процессорной системы.

Характер изменения вероятностей P_n при изменении суммарной загрузки четырехпроцессорной системы представлен на рис. 3.39.

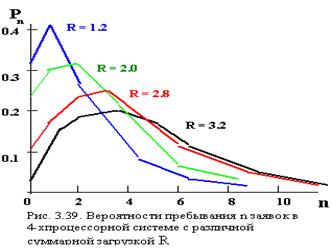
Распределение числа заявок в системе носит унимодальный характер, причем с увеличением загрузки максимальное значение P_n сдвигается в сторону больших N. Распределение (3.51) содержит всю информацию, необходимую для определения характеристик МПС. Средняя длина очереди заявок, ожидающих обслуживания в N-процессорной системе находится исходя из (3.51) как математическое ожидание случайной величины i=n-N>0, равной числу заявок в очереди:

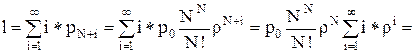
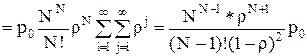, (3.53)

где р₀ определяется из (3.52).

Среднее число заявок, пребывающих в системе

m=l+R, (3.54)

где l – среднее число заявок, находящихся в очереди и определяемое (3.53); R – суммарная загрузка МПС, определяемая из (3.50).

Для систем без потерь заявок среднее время ожидания и среднее время пребывания заявок в системе равны соответственно w=l/ 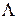и u=m/ 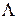. Подставляя в эти соотношения выражения (3.53) и (3.54), получим:

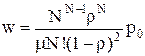; (3.55)

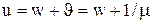(3.56)

или с использованием (3.50)

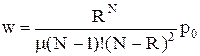(3.57)

Одна из важных характеристик системы – вероятность ненулевого ожидания заявок Pr (3.w>0), т.е. вероятность того, что в момент поступления очередной заявки все N процессоров заняты обслуживанием. Эта вероятность

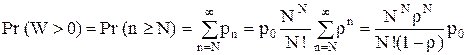(3.58)

Из сравнения (3.55) и (3.58) вытекает следующее выражение для среднего времени ожидания заявок:

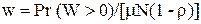(3.59)

В свою очередь, вероятность нулевого ожидания заявок, т.е. вероятность того, что в момент поступления заявки хотя бы один процессор свободен, равна Pr (3.W=0) = 1-Pr (3.W>0).