Аналогично для n переменных
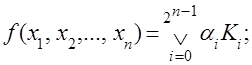 (3.3)
(3.3)
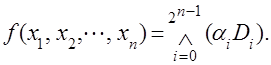 (3.4)
(3.4)
Здесь символ Ú обозначает логическую сумму (дизъюнкцию), а Ù - логическое произведение (конъюнкцию).
Последнее выражение позволяет легко перейти от таблицы истинности логической функции к аналитическому представлению. Поскольку 0 × Кi =0 и 1× Кi=Кi для представления функции в виде (3.3) нужно выписать дизъюнкцию тех Кi, для которых ai=1. Для логической функции, приведенной в табл.3.1. это будет выражение
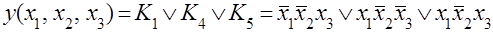
Последнюю формулу можно получить непосредственно из таблицы истинности, фиксируя внимание только на тех наборах, для которых У=1, и заменяя в них Хi=0 переменной 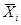 , а Хi=1 – переменной
, а Хi=1 – переменной 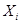 . Полученные таким образом полные конъюнкции нужно объединить знаком Ú. Описанный вид аналитического представления функции носит название совершенной дизъюнктивной нормальной формы (СДНФ). Из способа её построения следует, что каждая функция может иметь лишь единственное представление такого вида.
. Полученные таким образом полные конъюнкции нужно объединить знаком Ú. Описанный вид аналитического представления функции носит название совершенной дизъюнктивной нормальной формы (СДНФ). Из способа её построения следует, что каждая функция может иметь лишь единственное представление такого вида.
Дата добавления: 2015-10-05; просмотров: 970;
