В этих важных зависимостях имеются определенные закономерности, которые будет легче выявить, если ввести дополнительные обозначения.

Конъюнкцию всех аргументов функции ( с отрицанием или без) будем называть полной и обозначать буквой К с соответствующим индексом. Индексом в обозначении служит номер набора или двоичное число ( а также соответствующее ему десятичное), полученное при замене каждой переменной 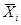- символом 0. Например, полной конъюнкции Х₁Х₂ соответствует индекс 11 (или 3) и обозначение К₃, а полной конъюнкции 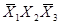- индекс 010 (или 2) и обозначение К₂. и т. д.

Дизъюнкцию всех аргументов функции (с отрицанием или без) будем называть полной и обозначать буквой D с индексом. Индекс здесь определяется иначе, чем для полной конъюнкции: путем замены переменной 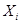на 0, и 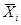- на 1. Поэтому полной дизъюнкции 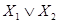соответствует индекс 00 (или 0) и обозначение D₀, а полной дизъюнкции 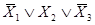- индекс 101 (или 5) и обозначение D₅.

Символы К_iи D_i однозначно определяют полную конъюнкцию и полную дизъюнкцию, если известно число переменных n.

Значение функции для конкретных наборов значений аргументов удобно обозначать символом a с индексом в виде десятичного числа, соответствующего двоичному числу, определяемому значениями аргументов, например:

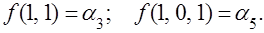
Вводя обозначения, формулы (3.1) и (3.2) для функции двух переменных можно записать в виде:

<3 4 567 8 9 >

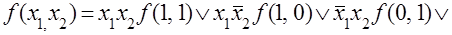
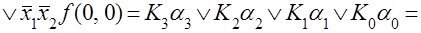
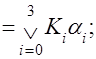
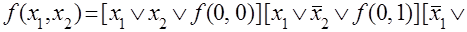
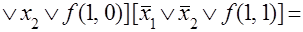
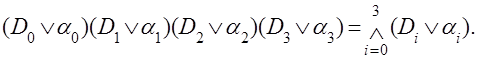
Дата добавления: 2015-10-05; просмотров: 1140;