Выражение СДНФ из вышеприведенного примера можно упростить следующим способом
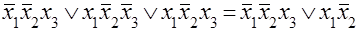 .
.
В случае сложных функций от большого числа переменных нахождение соседних выражений и их склеивание указанным выше способом становится затруднительным. Метод матриц Карно (диаграмм Вейча) облегчает процедуру склеивания благодаря тому, что соседние члены СДНФ или СКНФ, для которых возможно склеивание, размещаются на плоскости по соседству в географическом смысле. Для функций n переменных каждая составляющая канонической формы может иметь n соседей. Примеры матриц Карно приведены на рис. 3.2 - 3.4.
X2 X2 X3

 0 1 00 01 11 10
0 1 00 01 11 10





 X1 X1
X1 X1
0 0 1 0 0 1 3 2
 |  |
1 2 3 1 4 5 7 6
Рис.3.2 - Карты Карно для двух и трех переменных
 X3 X4
X3 X4
X1 X2 00 01 11 10
 |
 0 1 3 2
0 1 3 2
01 4 5 7 6


11 12 13 15 14
 |
8 9 11 10
Рис. 3.3 - Карта Карно для четырех переменных
 X3 X4 X5
X3 X4 X5
X1 X2 000 001 011 010 110 111 101 100
 |
00 0 1 3 2 6 7 5 4
 |
01 8 9 11 10 14 15 13 12
 |
11 24 25 27 26 30 31 29 28
 |
 10 16 17 19 18 22 23 21 20
10 16 17 19 18 22 23 21 20
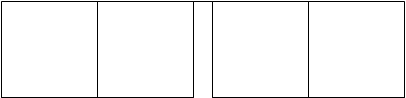
Рис. 3.4 – Карта Карно для пяти переменных
Каждая клетка матрицы соответствует одной комбинации значений входных переменных. Код этих комбинаций подобран так, чтобы соседние клетки отличались значением только одной переменной, т. е. чтобы им соответствовали соседние выражения. Код с таким свойством называется кодом Грея. В построенную на основе такого кода таблицу вписываются символы, соответствующие значениям функции на определенных наборах входных переменных из таблицы истинности.
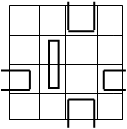
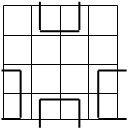
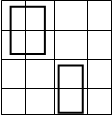
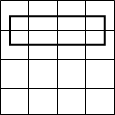
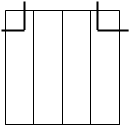
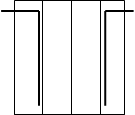
Если в двух соседних клетках заполненной матрицы Карно находятся одинаковые символы (0 или 1), то соответствующие этим клеткам выражения можно склеивать, что равносильно устранению переменной, которая в рамках склеиваемой группы меняет значения. Соседние клетки, образующие пары, объединяются замкнутой линией для обозначения возможности склеивания. Возможные варианты склеивания для функций четырех переменных приведены на рис. 3.5.
Рассмотрим пример. Пусть из таблицы истинности получена СДНФ и она минимизируется аналитическим методом посредством склеивания:
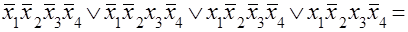
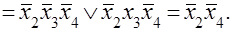
Матрица Карно для данного случая будет иметь вид, показанный на рис. 3.6.
 |  | ||||||||||
 |  | ||||||||||
 | |||||||||||
 |



 |  | ||||||||||
 |  | ||||||||||
 |  | ||||||||||
 |  | ||||||||||
Рис. 3.5 - Варианты склеивание для логической функции четырех переменных.
00 01 11 10









 00
00
 1 0 0 1
1 0 0 1
01 0 0 0 0
 |


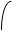

 11 0 0 0 0
11 0 0 0 0
1 0 0 1
 10
10
Рис.3.6 - Карта Карно для примера
Методика минимизации логических функций с помощью карт Карно используется при автоматизированном проектировании узлов современных ЭВМ и разработке логических моделей объектов и процессов горно-металлургического производства.
Основные понятия теории конечных автоматов
Конечным автоматом называется система S={A, Q ,V, d, l}, в которой A={a1,…,am}, Q={q1,…qn}, V={v1,…,vk} - конечные множества (алфавиты); a d : Q x A Þ Q и l : Q x A Þ V - функции, определенные на этих множествах. А называется входным алфавитом, V - выходным алфавитом, Q - алфавитом состояния; d – функцией переходов, l – функцией выходов. Если, кроме того, в автомате S выделено одно состояние, называемое начальным (будем считать, что это состояние q0), то полученный автомат называется инициальным и обозначается ( S ,q0 ) ; таким образом, по не инициальному автомату с n состояниями можно n различными способами определить инициальный автомат.
Поскольку функции d и l определены на конечных множествах, их можно задавать таблицами. Обычно две таблицы сводятся в одну таблицу d и l, называемую таблицей переходов - выходов автомата или автоматной таблицей.
Пример. Таблица 3.5 задает функции переходов и выходов для автомата с алфавитами A = { a1, a2, a3}, Q = {q1, q2, q3, q4}, V = {v1, v2}.
Таблица 3.5 - Табличное задание конечного автомата
| a1 | a2 | a3 | |
| q1 | q3 / v1 | q3 / v2 | q2 / v1 |
| q2 | q4 / v1 | q1 / v1 | q1 / v1 |
| q3 | q2 / v1 | q3 / v1 | q3 / v2 |
| q4 | q4 / v1 | q2 / v1 | q1 / v2 |
Еще один распространенный и наглядный способ задания автоматов – ориентированный мультиграф, называемый графом переходов или диаграммой переходов. Вершины графа соответствуют состояниям; если d (qi, aj) = qk и l (qi, aj)= vl, то из qi в qk ведет ребро, на котором написаны aj и vl . Граф переходов для таблицы 3.5 изображен на рис. 3.7. Кратные ребра не обязательны; например два ребра из q2 в q1 можно заменить одним, на котором будут написаны обе пары a3/v1 и a2/v1 . Для любого графа переходов в каждой вершине qi выполнены следующие условия, которые называются условиями корректности:
1) для любой входной буквы ai имеется ребро, выходящее из qi , на котором написано aj (условие полноты);
2) любая буква aj встречается только на одном ребре, выходящем из qi (условие непротиворечивости или детерминированности).
Для данного автомата S его функции dS и lS могут быть определены не только на множестве А всех выходных букв, но и на множестве А* всех входных слов. Для любого входного слова a = (aj1, a j2,..., ajk); d( qi, aj1, aj2,…, ajk ) = d ( d( ...d( qi, aj1), aj2) ,…, ajk-1), ajk).
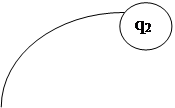 | |||
| |||
|
 |
Рис.3.7 - Граф конечного автомата
Другим способом это традиционное определение можно представить следующим образом:
1) d ( qi , aj ) задается автоматной таблицей S;
2) для любого слова a Î А* и любой буквы аj
d( qi, aaj ) = d ( d( qi, a ), aj).
Дата добавления: 2015-10-05; просмотров: 1555;
