Здесь и в дальнейшем символы состояний для кратности обозначений будут заменяться их индексами.
С помощью расширенной функции d определяется (индуктивно) расширенная функция l.
l(qi, aaj) = l ( d ( qj , a), aj).
Зафиксируем в автомате S начальное состояние q1 и каждому входному слову a = аj1, аj2, …, аjk поставим в соответствие слово w в выходном алфавите:
w = l ( q1, aj1) l ( q1,aj1aj2 ) ... l ( q1,aj1,…,ajk ).
Это соответствие, отображающее входные слова в выходные слова называется автоматным отображением, а так же автоматным оператором. Если результатом применения оператора к слову a является выходное слово w, то это будем обозначать соответственно S (q1, a)= w или S( a )= w. Число букв в слове a, как обычно является длиной a и обозначается ½a ½или l(a).
Автоматное отображение обладает следующими свойствами:
- слова a и w = S( a) имеют одинаковую длину;
- если a = a1a2 и S(a1a2)= w1w2 , где a1= w1 , то S( a1 )= w1 ;
Последнее свойство отражает тот факт, что автоматные операторы – это операторы, которые перерабатывая слово слева направо не «заглядывают вперед». При этом i – я буква выходного слова зависит только от первых i - букв выходного слова.
Указанные свойства были бы достаточными условиями автоматного отображения, если бы речь шла о бесконечных автоматах. Для конечных автоматов этих условий недостаточно при реализации для произвольных входных и выходных алфавитов.
Абстрактная и структурная теория конечных автоматов
Под автоматом понимается устройство, самостоятельно производящее все операции. Формальное описание автомата называют его логической структурой. Свойства и методы преобразования логических структур изучает теорию конечных автоматов, которая подразделяется на абстрактную и структурную. Абстрактная теория не затрагивает структуру самого автомата, ограничиваясь лишь рассмотрением переходов, претерпеваемых автоматом при изменении входных сигналов, выдаваемых автоматом в каждом состоянии. Структурная теория изучает способы построения автоматов, их структуру, способы кодирования входных и выходных сигналов.
Автомат называется комбинационным, если для любого входного символа а и любых состояний qi и qj l(qi, a)= l(qj, a), иначе говоря, если выходной символ не зависит от состояния и определяется текущим входным символом. В таком автомате все состояния эквивалентны и, следовательно, минимальный комбинационный автомат имеет одно состояние. Функция переходов в нем вырождена и его поведение однозначно задается функцией выходов с одним аргументов: l(ai)=vi.
Все автоматы можно подразделить на синхронные и асинхронные. Известны две модели синхронных элементарных автоматов: модель Мура и модель Мили, получившие названия по именам ученых, разработавших соответствующие разделы теории автоматов. Моделью Мура называется автомат, описываемый уравнениями:
q(t) =d[x(t-1); q(t-1)]; v(t)=l[q(t)],
где q(t), q(t-1) - состояния автомата в моменты времени t и t-1; x(t-1), v(t) - входной и выходной сигналы автомата в моменты времени t и t-1.
Для модели Мили справедливы соотношения:
q(t) =d[x(t-1); q(t-1)];
v(t)=l[x(t); q(t)].
Существует несколько способов представления конечных автоматов, основными из которых является графический, таблично - матричный, аналитический с использованием секвенциальных уравнений. Пусть необходимо синтезировать автомат, разрешающий работу некоторого устройства при наличии единичных сигналов на входах Х1, Х2 , причем, для включения устройства необходимо выполнить условие появления сигнала на входе Х1 раньше, чем на входе Х2. При графическом способе описания данный автомат можно представить в виде направленного графа (рис. 3.8 и 3.9), вершинами которого являются состояния автомата, а ребрами - комбинации выходных сигналов.
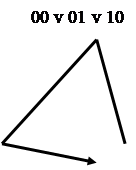 | 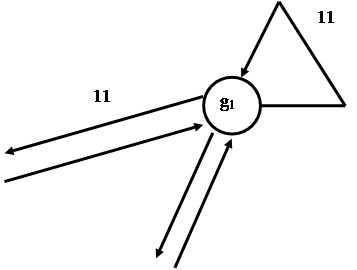 | ||
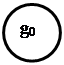
|
| |
| |

Рис. 3.8 - Граф автомата Мура
 | |||
| |||
Рис.3.9 - Автомат Мили.
Как видно из графа, комбинация (01) вызывает переход автомата из некоторого состояния S0 в состояние S1, соответствующее появлению единичного сигнала на выходе У автомат может перейти только из состояния S1 при условии поступления комбинации входных сигналов Х1, Х2 (11). Данный граф соответствует представлению автомата моделью Мура т.к. выходной сигнал (указан в узлах графа) полностью определяется внутренним состоянием автомата и не зависит от комбинации сигналов на входе. При задании автомата моделью Мили его выходной сигнал указывается над каждым ребром графа (см. рис. 3.4), т.к. зависит не только от внутреннего состояния автомата, но и от комбинации сигналов, поступающих на вход автомата в данный момент времени.
Вместо построения графа всю необходимую информацию о работе можно свести в специальные автоматные таблицы: таблицу переходов и таблицу выходов. Представление автомата при помощи таблиц показано в таблицах 3.6 - 3.9.
Таблица 3.6 - Таблица переходов автомата Мура
| Состояния | Входные сигналы | ||||||
| g0 | g0 | g0 | g1 | g0 | |||
| g1 | g0 | g0 | g1 | g2 | |||
| g2 | g0 | g0 | g1 | g2 | |||
Таблица 3.7 - Таблица выходов автомата Мура
| Состояние | g0 | g1 | g2 |
| Выходные сигналы |
Таблица 3.8 - Таблица переходов автомата Мили
| Состояния | Входные сигналы | ||||||
| g0 | g0 | g0 | g1 | g0 | |||
| g1 | g0 | g0 | g1 | g1 | |||
Таблица 3.9 - Таблица выходов автомата Мили
| Состояния | Выходные сигналы | ||||||
| g0 | |||||||
| g1 | |||||||
На пересечении строк и столбцов автоматных таблиц указываются внутренние состояния, в которые переходит автомат под действием входных сигналов и выходные сигналы, которые он при этом выдает. Обе рассмотренных формы задания автоматов построены для одного и того же примера автоматов Мура и Мили.
Дата добавления: 2015-10-05; просмотров: 1005;
