При поиске представления функции вида (3.4) нужно учитывать, что

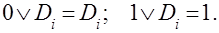
Поэтому в соответствующем выражении нужно оставить конъюнкция только тех D_i, для которых a_i = 0. Для рассматриваемого примера это выражение это выражение имеет вид:

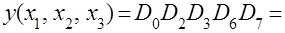
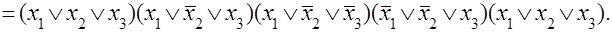
Последнюю формулу можно получить непосредственно из таблицы истинности, выбирая из нее только те наборы, для которых У = 0, и заменяя в них те наборы, для которых У = 0, и заменяя в них Х_i = 0. Переменной Х_i, а Х_i = 1 – переменной 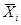. Полученные полные дизъюнкции соединяются знаками конъюнкции. Такой вид представления носит название совершенной конъюнктивной нормальной формы (СКНФ). Для каждой функции он также единствен.

3.4. Задача минимизации логических функций

Если в составе проектируемой схемы должны входить элементы И, ИЛИ, НЕ то представление функций в любой из рассмотренных канонических форм уже дает возможность построения такой схемы. Легко подсчитать, какое количество и каких элементов потребуется для реализации конкретной логической функции. На рассмотренном выше примере видно, что использование СДНФ даст более простую реализацию.

Принимая во внимание подобные проблемы оптимизации проектируемого устройства, можно утверждать, что в общем случае схема с меньшим количеством элементов обходится дешевле и более надежна в работе. Следовательно, независимо от применяемых при построении логических схем элементов, важным этапом синтеза является поиск такого вида логической функции, в котором имеется минимальное число логических операций над минимальным числом входных сигналов. Процесс поиска такого вида называется минимизацией функции и основывается на так называемых правилах склеивания:

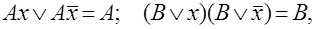
в которых А и В – переменные или логические функции. Эти правила можно сформулировать следующим образом: дизъюнкция или конъюнкция двух переменных, отличающихся одно от другого только знаком отрицания для одной переменной, могут быть заменены одним выражением без той переменной, по которой они отличаются. Например:

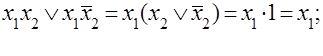
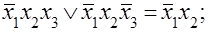
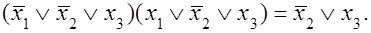
Выражения, для которых возможно склеивание, называют соседними выражениями. Если в полученных канонических представлениях имеются соседние выражения, то соответствующие представления можно упростить с целью получения простой технической реализации