Производная по направлению. Градиент
Производной функции 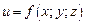 в точке
в точке 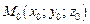 по направлению
по направлению 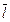 называется предел
называется предел
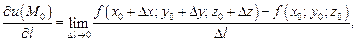
где 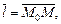
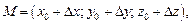
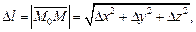
если предел существует.
Если функция 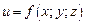 дифференцируема, то производная по направлению вычисляется по формуле
дифференцируема, то производная по направлению вычисляется по формуле
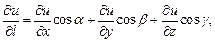 (18.31)
(18.31)
где 

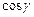 – направляющие косинусы вектора
– направляющие косинусы вектора 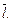
В частности, если 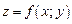 – функция двух переменных, то формула (18.31) производной по направлению примет вид:
– функция двух переменных, то формула (18.31) производной по направлению примет вид:
 (18.32)
(18.32)
где  – угол между вектором
– угол между вектором 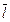 и осью Ох.
и осью Ох.
Градиентом функции 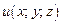 в точке
в точке 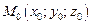 называется вектор
называется вектор
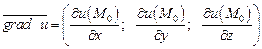 (18.33)
(18.33)
или, то же самое,

Связь между градиентом функции и производной по направлению устанавливает формула
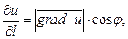
где 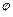 – угол между векторами
– угол между векторами 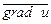 и
и 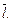
Градиент функции указывает направление наибыстрейшего возрастания функции. Наибольшее значение производной  достигаемое в направление градиента, равно
достигаемое в направление градиента, равно
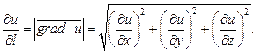
В частности, если 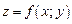 – функция двух переменных, то
– функция двух переменных, то
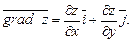
Пример 1. Найти производную функции 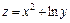 в точке
в точке 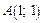 по направлению вектора
по направлению вектора 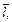 образующего с положительным направлением оси Ох угол
образующего с положительным направлением оси Ох угол 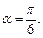
Решение.Используя формулу (18.32),вычислим частные производные функции z в точке A:
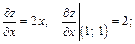

Так как 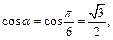
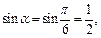 то
то
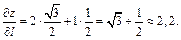
Пример 2. Найти производную функции 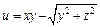 в точке
в точке  по направлению к точке
по направлению к точке 
Решение.Найдем вектор 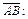
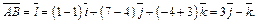
Его направляющие косинусы равны:
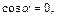
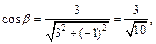
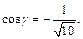
Найдем значения частных производных функции u в точке 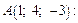

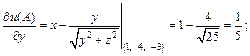

Тогда по формуле (18.31) получим:
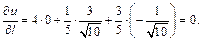
Пример 3.Найти длину и направление (указать направляющие косинусы) градиента функции 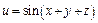 в точке
в точке 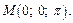
Решение.Вычислим частные производные функции u в точке М.
Используем формулу (18.33) при условии, что частные производные вычисляем в заданной точке 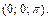
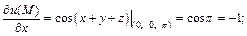

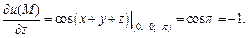
Тогда 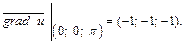
Вычисляем длину полученного вектора:
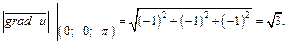
Используем тот факт, что направляющие косинуса равны координатам единичного вектора направления, определяемого вектором дроби. Поэтому
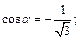
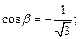
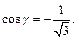
Дата добавления: 2015-09-29; просмотров: 1884;
