Горизонтальный барический градиент
Рассмотрим в атмосфере прямоугольный параллелепипед с ребрами dx, dy, dz (рис. 5.12). Нас интересует изменение давления в горизонтальном направлении, т.е. вдоль оси х.
Пусть изобара с давлением р направлена параллельно оси y, вдоль ребра 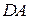 . Параллельно ей вдоль ребра СВ проходит изобара с давлением (p + dp). Напомним, что атмосферное давление характеризуется силой, действующей на единицу площади поверхности, нормально последней. В дальнейшем пренебрегаем временными изменениями давления, т.е. рассматриваем его изменение только в пространстве.
. Параллельно ей вдоль ребра СВ проходит изобара с давлением (p + dp). Напомним, что атмосферное давление характеризуется силой, действующей на единицу площади поверхности, нормально последней. В дальнейшем пренебрегаем временными изменениями давления, т.е. рассматриваем его изменение только в пространстве.
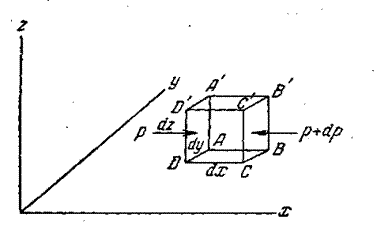 |
Рис/ 5.12. К расчету силы горизонтального градиента давления
Итак, слева на грань AA'D'D атмосферное давление равно р. На противоположную грань ВВ'C'C давление равно 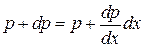 . Так как сила, действующая на всю грань, равна произведению атмосферного давления на ее площадь, запишем выражение для силы:
. Так как сила, действующая на всю грань, равна произведению атмосферного давления на ее площадь, запишем выражение для силы:
· слева рdydz,
· справа  .
.
В результате на объем dxdydz действует сила (dFx), равная
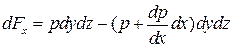 ,
,
или 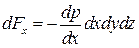 . (5.1)
. (5.1)
Согласно второму закону Ньютона, сила dFx и масса рассматриваемого объема
dm = рdxdydz (5.2)
связаны между собой (отношение силы к массе равно ускорению а):
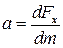 , (5.3)
, (5.3)
откуда, с учетом (5.1) и (5.2)
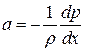 . (5.4)
. (5.4)
Мы получили выражение для ускорения а, которое создает сила барического градиента. Величина его, согласно (5.3), равна силе барического градиента, приходящейся на единицу массы элементарного объема воздуха. Знак минус в формуле (5.1) и (5.4) указывает, что сила и ускорение барического градиента направлены в сторону убывания давления. Причем сила и ускорение барического градиента действуют в направлении наиболее быстрого убывания давления. Таким направлением является направление нормали к изобаре в рассматриваемой точке приложения силы.
В (5.4) выражение 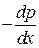 равно численной величине барического градиента. Горизонтальный барический градиент можно графически представить стрелкой, направленной по нормали к изобаре в сторону убывания давления. Длина стрелки должна быть пропорциональна числовой величине градиента (рис. 5.13). Иначе говоря, величина горизонтального барического градиента обратно пропорциональна расстоянию между изобарами.
равно численной величине барического градиента. Горизонтальный барический градиент можно графически представить стрелкой, направленной по нормали к изобаре в сторону убывания давления. Длина стрелки должна быть пропорциональна числовой величине градиента (рис. 5.13). Иначе говоря, величина горизонтального барического градиента обратно пропорциональна расстоянию между изобарами.
Очевидно, что там, где изобары сгущены, барический градиент, т.е. изменение давления на единицу расстояния по нормали к изобаре, – больше. Там, где изобары раздвинуты, барический градиент меньше.
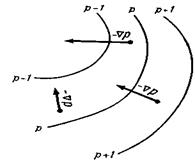
Рис. 5.13. Стрелки обозначают горизонтальный барический градиент в трех точках барического поля
Изобарические поверхности наклонены всегда в направлении градиента, т.е. в направлении, куда давление убывает (рис. 5.13).
Вертикальный барический градиент (см. гл. 1) в десятки тысяч раз больше горизонтального. Далее речь пойдет только о горизонтальном барическом градиенте. Для определения среднего барического градиента для участка барического поля измеряют давление вдоль нормали к изобарам в двух точках, расположенных на расстоянии, соответствующем одному градусу меридиана (111 км). Барический градиент численно равен разнице давлений 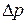 и имеет размерность мб/111 км (или гПа/111 км). В атмосфере у земной поверхности порядок величины горизонтальных барических градиентов составляет несколько миллибар (чаще 1–3) на каждый градус меридиана (111 км).
и имеет размерность мб/111 км (или гПа/111 км). В атмосфере у земной поверхности порядок величины горизонтальных барических градиентов составляет несколько миллибар (чаще 1–3) на каждый градус меридиана (111 км).
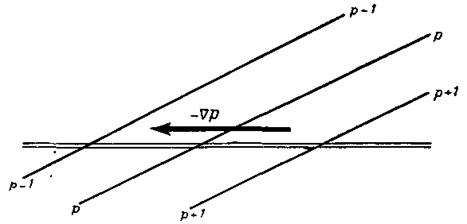
Рис. 5.14. Вертикальный разрез изобарических поверхностей. Стрелка – направление горизонтального барического градиента; двойная линия – поверхность уровня
Например, пусть на синоптической карте масштаба 1: 10 000 000 расстояние между соседними изобарами составляет 2 см. Шаг изолиний 5 мб. Для указанного масштаба 2 см на карте соответствуют 200 км в натуре. Следовательно, разница давлений на 100 км составит 5/2= 2.5 мб/100 км. Для расстояния 111 км эта разница 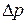 =
= 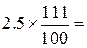 2.75 мб/111 км.
2.75 мб/111 км.
Если бы в атмосфере действовала только сила горизонтального барического градиента, то воздух двигался бы равноускоренно, с ускорением, которое можно рассчитать по формуле (5.4). Ускорение при реальных градиентах давления составляет небольшую величину, порядка 0–0.3 см/с2. Тем не менее с ростом продолжительности действия силы барического градиента, скорости ветра бы неограниченно возрастали. В действительности скорости ветра редко превышают 10 и более м/с. Следовательно, действуют также другие силы, уравновешивающие силу барического градиента (об этом – в следующей главе).
Изменение барического градиента с высотой связаны с неравномерным распределением температуры. Следуя С.П. Хромову [84], представим себе, что у земной поверхности барический градиент равен нулю т.е. давление во всех точках одинаково (рис. 5.15). При этом температура в одной части рассматриваемой области выше, в другой ниже. Горизонтальный температурный (термический) градиент по определению  T,всегда направлен по нормали к изотерме (линии равных температур) в ту сторону, куда температура возрастает.
T,всегда направлен по нормали к изотерме (линии равных температур) в ту сторону, куда температура возрастает.
Вспомним, что давление падает с высотой тем быстрее, чем ниже температура воздуха. Отсюда следует, что изобарические поверхности при неравномерном распределении температуры не могут быть горизонтальными. Если даже приземная изобарическая поверхность горизонтальна, то каждая вышележащая изобарическая поверхность будет приподнята над нижележащей поверхностью в холодном воздухе меньше, в теплом воздухе больше. Это означает, что вышележащие поверхности будут наклонены от теплого воздуха к холодному (рис. 5.15). Таким образом, хотя у земной поверхности горизонтальный барический градиент нулевой, в вышележащих слоях такой градиент имеется.

|

Xолод Tепло
Рис. 5.15. Связь между горизонтальными градиентами температуры и давления
Более того, каков бы ни был горизонтальный барический градиент у земной поверхности, с высотой он будет по своему направлению приближаться к горизонтальному температурному градиенту. На достаточно большой высоте горизонтальный барический градиент будет близко совпадать по направлению со средним горизонтальным градиентом температуры в слое воздуха от нижнего уровня до верхнего. Из рис. 5.15 следует, что в теплых областях атмосферы давление на заданной высоте будет повышенным, а в холодных областях пониженным.
Основываясь на основном уравнении статики атмосферы, можно получить уравнение, связывающее барические градиенты на верхнем z2 и нижнем z1 уровнях (вывод можно найти в [84,83]):
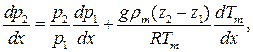 (5.5)
(5.5)
где 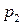 ,
, 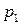 – атмосферное давление на рассматриваемых уровнях;
– атмосферное давление на рассматриваемых уровнях;  ,
,  – соответственно средняя плотность и средняя температура воздуха в слое между указанными уровнями;
– соответственно средняя плотность и средняя температура воздуха в слое между указанными уровнями; 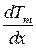 – горизонтальный градиент средней температуры воздуха.
– горизонтальный градиент средней температуры воздуха.
Второй член правой части уравнения (5.5) характеризует дополнительную составляющую горизонтального барического градиента, пропорциональную градиенту температуры. Эта составляющая увеличивается с увеличением толщины слоя 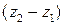 и возрастания горизонтального градиента температур
и возрастания горизонтального градиента температур 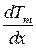 . Начиная с некоторой высоты, направления горизонтального градиента температуры и давления практически совпадут.
. Начиная с некоторой высоты, направления горизонтального градиента температуры и давления практически совпадут.
Дата добавления: 2015-09-07; просмотров: 6489;
