Градиент и его свойства.

Определение. Скалярное поле u(M) называют дифференцируемым в 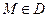, если существует окрестность 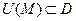и существует вектор g, что для любой 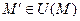приращение 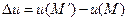имеет вид

,

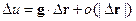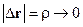
Утверждение. Если такое представление существует, то оно единственно.

Определение. Вектор g из 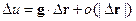называется градиентом скалярного поля u(M) и обозначается 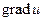или .

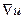Рассмотрим открытое множество 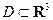, фиксированную точку 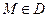, фиксированный единичный вектор l, .

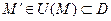Определение. Если существует 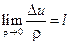, где 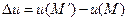, , 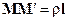то число l называют производной по направлению l и обозначают .

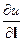Утверждение. Если скалярное поле u(M) дифференцируемо в точке 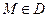, то для любого единичного вектора l существует .

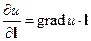В декартовой системе координат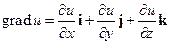

Свойства

,

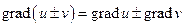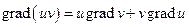
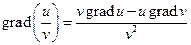
Определение криволинейного интеграла первого рода

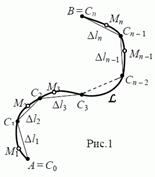Пусть дана (неориентированная) линия L с концами точках А и В и функция трех переменных f(x, y, z) = f(M),определенная в каждой точке 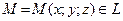.Разобьем линию L на п (необязательно равных) частей точками А = С₀, С₁, С₂, ..., C_n-1, C_n = B.Выберем на каждой дуге C_k-1C_k произвольную точку 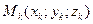, обозначим через 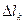длину хорды 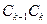, k = 1, 2, ..., n и пусть 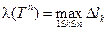− мелкость полученного разбиения Tⁿ линии L (см. Рис.1).

Составим интегральную сумму 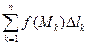. Если существует конечный предел таких интегральных сумм при стремлении мелкости разбиения к нулю ( 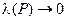),не зависящий от способа разбиения линии L на п частей и выбора точек С_k. то этот предел называется криволинейным интегралом первого родаот функции f(x, y, z)по линии L,и обозначается:

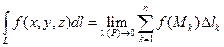
Теорема. Если линия L имеет кусочно-гладкую параметризацию, а функция f(x, y, z) = f(M)непрерывна на ней, то существует криволинейный интеграл первого рода .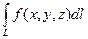

Свойства криволинейного интеграла первого рода:

(1) аддитивность; (2) линейность; (3) переход к неравенству под знаком интеграла; (4) интеграл от константы; (5) теорема об оценке; (6) теорема о среднем (для непрерывного пути L и непрерывной функции f).