Градиент

По определению градиентом скалярной функции 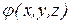называется вектор

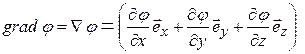. (13.01)

Следует помнить о том, что градиента векторной функции не существует, в силу того, что он просто не определен. Можно рассматривать градиент модуля вектора, но модуль – это скалярная величина.

Физический смысл градиента функции заключается в том, что это вектор, направленный в сторону скорейшего возрастания функции, а по модулю равный производной, взятой вдоль направления скорейшего возрастания.

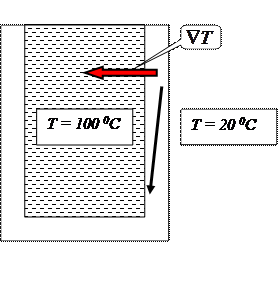
НАПРИМЕР, если в стакан налит кипяток, то, очевидно, что в стенках стакана устанавливается градиент температуры. Поскольку градиент направлен в сторону скорейшего возрастания величины, то градиент температуры перпендикулярен стенкам стакана. Температура изменяется и вдоль направления черной стрелки, но направление СКОРЕЙШЕГО возрастания задается, очевидно, красной.

Величину градиента грубо можно оценить, разделив известное изменение величины на расстояние на котором оно происходит, если это расстояние в направлении скорейшего изменения.

Пока стенки не прогрелись по толщине, можно считать, что на внутренней поверхности температура 100 ⁰С, а на внешней – в соответствии с температурой окружающей среды – 20⁰С. Если толщина стенок 1 мм, то градиент по модулю равен 80 ⁰С/мм = 8 10^{4 0}С/м. По мере прогревания стенок температура воды в стакане немного упадет, но на внешней поверхности – сильно возрастет. Разница температур уменьшится и градиент по модулю тоже.

Сравним понятия градиент и скорость. Когда мы говорим «скорость изменения некоторой величины равна…», то обычно подразумеваем, что речь о быстроте изменения величины во времени. Говоря о том, что градиент некоторой величины составляет столько-то, мы говорим о быстроте изменения величины в пространстве, т.е. при изменении пространственных координат.