Градиент функции

Из школьного курса математики известно, что вектор на плоскости представляет собой направленный отрезок. Его начало и конец имеют по две координаты. Координаты вектора рассчитываются путем вычитания из координат конца координат начала.

Понятие вектора может быть распространено и на n-мерное пространство (вместо двух координат будет n координат).

Градиентом grad z функции z = f(х₁, х₂, …х_n) называется вектор частных производных функции в точке, т.е. вектор с координатами .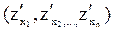

Можно доказать, что градиент функции характеризует направление наискорейшего роста уровня функции в точке.

Например, для функции z = 2х₁ + х₂ (см. рисунок 5.8) градиент в любой точке будет иметь координаты (2; 1). Построить его на плоскости можно различными способами, взяв в качестве начала вектора любую точку. Например, можно соединить точку (0; 0) с точкой (2; 1), или точку (1; 0) с точкой (3; 1), или точку (0; 3) с точкой (2; 4), или т.п. (см. рисунок 5.8). Все построенные таким образом вектора будут иметь координаты (2 – 0; 1 – 0) =
= (3 – 1; 1 – 0) = (2 – 0; 4 – 3) = (2; 1).

Из рисунка 5.8 хорошо видно, что уровень функции растет в направлении градиента, поскольку построенные линии уровня соответствуют значениям уровня 4 > 3 > 2.

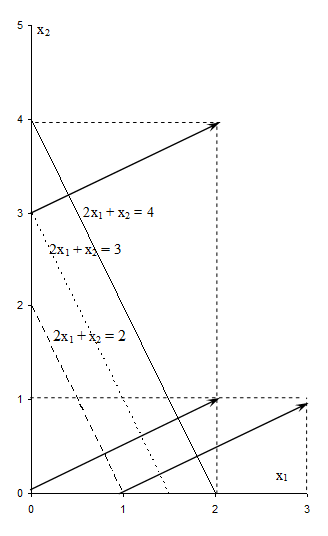
Рисунок 5.8 - Градиент функции z = 2х₁ + х₂

Рассмотрим другой пример – функцию z = 1/(х₁х₂). Градиент этой функции уже не будет всегда одинаковым в разных точках, поскольку его координаты определяются формулами (-1/(х₁²х₂); -1/(х₁х₂²)).

На рисунке 5.9 представлены линии уровня функции z = 1/(х₁х₂) для уровней 2 и 10 (прямая 1/(х₁х₂) = 2 обозначена пунктиром, а прямая
1/(х₁х₂) = 10 – сплошной линией).

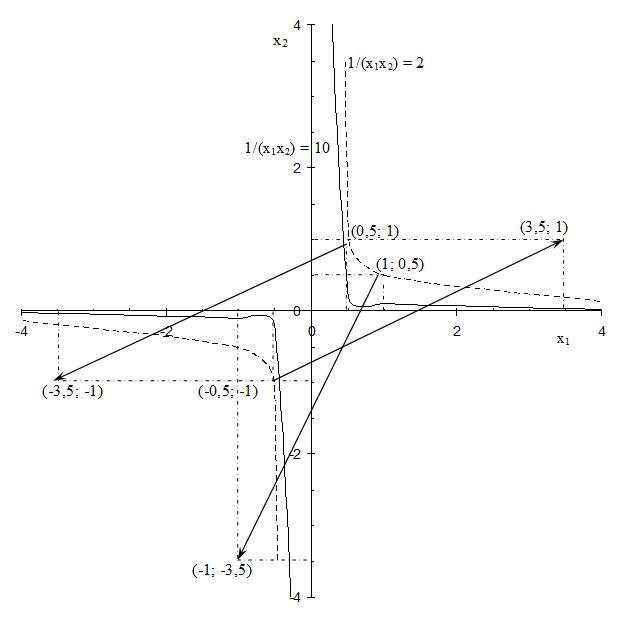
Рисунок 5.9 - Градиенты функции z = 1/(х₁х₂) в различных точках

Возьмем, например, точку (0,5; 1) и вычислим градиент в этой точке: (-1/(0,5²*1); -1/(0,5*1²)) = (-4; -2). Заметим, что точка (0,5; 1) лежит на линии уровня 1/(х₁х₂) = 2, ибо z = f(0,5; 1) = 1/(0,5*1) = 2. Чтобы изобразить вектор (-4; -2) на рисунке 5.9, соединим точку (0,5; 1) с точкой (-3,5; -1), ибо
(-3,5 – 0,5; -1 - 1) = (-4; -2).

Возьмем другую точку на той же самой линии уровня, например, точку (1; 0,5) (z = f(1; 0,5) = 1/(0,5*1) = 2). Вычислим градиент в этой точке
(-1/(1²*0,5); -1/(1*0,5²)) = (-2; -4). Чтобы изобразить его на рисунке 5.9, соединим точку (1; 0,5) с точкой (-1; -3,5), ибо (-1 - 1; -3,5 - 0,5) = (-2; -4).

Возьмем еще одну точку на той же самой линии уровня, но только теперь в неположительной координатной четверти. Например, точку (-0,5; -1) (z = f(-0,5; -1) = 1/((-1)*(-0,5)) = 2). Градиент в этой точке будет равен
(-1/((-0,5)²*(-1)); -1/((-0,5)*(-1)²)) = (4; 2). Изобразим его на рисунке 5.9, соединив точку (-0,5; -1) с точкой (3,5; 1), ибо (3,5 – (-0,5); 1 – (-1)) = (4; 2).

Следует обратить внимание, что во всех трех рассмотренных случаях градиент показывает направление роста уровня функции (в сторону линии уровня 1/(х₁х₂) = 10 > 2).

Можно доказать, что градиент всегда перпендикулярен линии уровня (поверхности уровня), проходящей через данную точку.