Выпуклость функции многих переменных

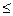
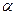
Функция f(X), заданная в выпуклой области, называетсявыпуклой вниз (вверх), если для любых точек Х⁽¹⁾, Х⁽²⁾ из области ее определения и любого числа 0 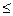1 выполняется:

f( 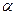X⁽¹⁾ + (1- 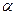)Х⁽²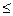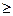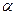⁾) ( ) f(X⁽¹⁾) + (1- 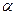)f(Х⁽²⁾)

Для функции одной переменной это означает, что выпуклая вверх функция лежит выше отрезка, соединяющего любые две точке ее графика, а выпуклая вниз – ниже.

Определение выпуклой функции уже давалось ранее при изучении исследования функций с помощью дифференциального счисления, только вместо формулы отрезка использовалась формула, определяющая середину отрезка (см. рисунок 3.7).

Если неравенства в определении выполняются, как строгие, то функция называется строго выпуклой. В соответствии с этим определением линейная функция является нестрого выпуклой одновременно вверх и вниз.

Для выпуклой функции равенство нулю частных производных является не только необходимым, но и достаточным условием экстремума. Т.е. если функция является строго выпуклой на всей рассматриваемой области, и получена стационарная точка, то в ней достигается глобальный максимум (при выпуклости вверх) или минимум (при выпуклости вниз).

Для отыскания глобального максимума (наибольшего значения) выпуклой вниз функции или глобального минимума (наименьшего значения) выпуклой вверх функции достаточно исследования экстремумов только на границе области определения.