Дифференциал функции многих переменных
Дифференциалом функции называют сумму произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е. 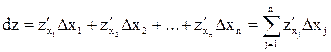 (n – число аргументов).
(n – число аргументов).
Для функции двух переменных z = f(x,y) дифференциал можно записать 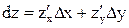 .
.
По-другому дифференциал записывается как 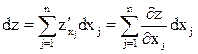 (для двух переменных
(для двух переменных 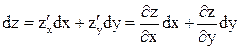 ).
).
Функция нескольких переменных z = f(х1, х2, …хn) = f (X) называется дифференцируемой в точке X, если ее полное приращение может быть представлено в виде 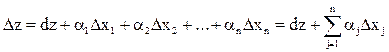 , где dz - дифференциал функции,
, где dz - дифференциал функции, 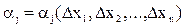 - бесконечно малые величины при Δхj ® 0.
- бесконечно малые величины при Δхj ® 0.
Таким образом, дифференциал функции нескольких переменных, как и в случае одной переменной, представляет собой главную, линейную относительно приращений аргументов, часть полного приращения функции.
Можно доказать, что если частные производные функции существуют в некоторой окрестности точки и непрерывны в самой точке, то функция дифференцируема в этой точке (достаточное условие дифференцируемости функции).
Дифференциалом функции многих переменных второго порядка называют сумму произведений частных производных второго порядка этой функции на приращения соответствующих независимых переменных: 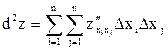 (n – число аргументов).
(n – число аргументов).
Для функции двух переменных z = f(x,y) дифференциал второго порядка можно записать 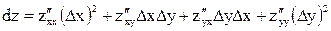 или
или 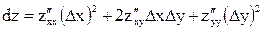 для непрерывных вторых производных.
для непрерывных вторых производных.
Дата добавления: 2015-10-06; просмотров: 851;
